PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoபல்லுறுப்புக்கோவையை எளிதில் காரணிபடுத்த முடியாத போது மட்டுமே நீள்வகுத்தல் முறை பயன்படுத்தப்படுகிறது. பொதுவாக, பல்லுறுப்புக்கோவையின் படி அதிகமாக இருக்கும் போது நீள்வகுத்தல் முறை பயன்படுத்தப்படுகிறது.
நீள்வகுத்தல் முறையைத் தொடங்கும் முன், கொடுக்கப்பட்ட பல்லுறுப்புக்கோவை மாறிகளின் படியானது ஏறுவரிசையிலோ அல்லது இறங்கு வரிசையிலோ எழுத வேண்டும்.
ஒரு பல்லுறுப்புக்கோவையின் வர்க்க மூலத்தை நீள்வகுத்தல் முறை மூலம் எவ்வாறு கண்டுபிடிப்பது என்பதைப் புரிந்துகொள்வோம்.
Example:
\(9x^4 + 12x^3 + 10x^2 + 4x + 1\) என்பதன் வர்க்கமூலம் காண்க.
தீர்வு:
படி 1: ஒன்றாம் இலக்கத்தில் இருந்து சோடியாக பிரிக்க. அதாவது, \(9x^4 + \overline{12x^3 + 10x^2} + \overline{4x + 1}\).
படி2: இங்கு, இடப்புறமுள்ள பெரிய எண் \(9x^4\). கொடுக்கப்பட்ட எண்ணுக்கு சமமான அல்லது குறைவான வர்க்கத்தை நாம் கண்டறிய வேண்டும். இங்கு, அந்த எண்ணின் வர்க்கம் \(3x^2\) ஆகும்.
ஆகவே,
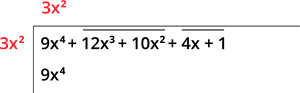
படி3: எண்களைக் கழித்தால், \(0\) கிடைக்கும், மேலும் அடுத்த சோடியை மீதியின் வலது பக்கம் எழுத வேண்டும்.
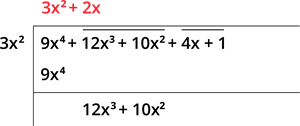
படி4: ஈவை \(2\) ஆல் பெருக்குவதன் மூலம் புதிய வகுத்தியை காணலாம். மேலும், \(12x^3 + 10x^2\) இல் உள்ள முதல் கோவையை கிடைக்கப்பெற்ற கோவையால் வகுப்பதன் மூலம் கிடைக்கும் ஈவை எடுதுக்கொள்வோம்.
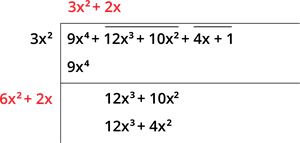
படி5: எண்களைக் கழித்து தீர்வை எழுதவும், மற்றும் அடுத்த சோடியை மீதமுள்ளவற்றை வலது பக்கம் எழுதுக.
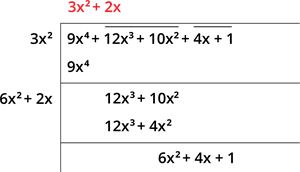
படி6: ஈவை \(2\) ஆல் பெருக்குவதன் மூலம் புதிய வகுத்தியைக் கண்டறியவும். மேலும்,
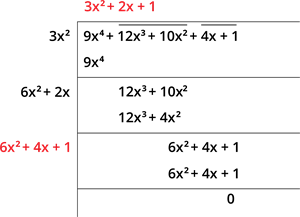
எனவே, \(\sqrt{9x^4 + 12x^3 + 10x^2 + 4x + 1} = |3x^2 + 2x + 1|\).
Register for free to see more content