PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo\(x\) இன் அதிகரிப்பு \(y\) (மற்றும் நேர்மாறாகவும்) விகிதத்தில் குறையும்போது இரண்டு அளவுகள் \(x\) மற்றும் \(y\) ஆகியவை எதிர் விகிதத்தில் காணப்படுகின்றன. அவற்றின் தொடர்புடைய மதிப்புகளின் பெருக்கற்பலன் மாறா எண்ணாக (நிலையானதாக) இருக்கும்.
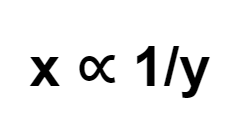
அதாவது, \(xy = k\), என்றால் \(x\) மற்றும் \(y\) ஆகியவை நோ்மாறான விகிதத்தில் மாறுபடும்.
\(x\) மற்றும் \(y\) அளவுகள் எதிா் விகிதத்தில் இருக்கும்போது, நாம் \(=\) அல்லது \(=\) என்று எழுதலாம். , என்பது \(x\)ன் , மதிப்புகளுடன் தொடா்புடைய \(y\) மதிப்புகள்.
ஒரு விவசாயி தனவு வயலில் \(6\) நாட்களுக்கு \(20\) கோழிகளுக்கு உணவளிக்கும் அளவுக்கு உணவு உள்ளது. அவருடைய வயலில் இன்னும் \(10\) கோழிகள் இருந்தால் உணவு எவ்வளவு காலம் நீடிக்கும்?
Example:
நாட்களின் எண்ணிக்கை \(x\).
கோழிகளின் மொத்த எண்ணிக்கை \(= 20\) \(+\) \(10 =\) \(30\).
கோழிகளின் எண்ணிக்கையில் அதிகரிப்பு உணவு நீடிக்கும் நாட்களின் எண்ணிக்கையை குறைக்கிறது.
இதனால், கோழிகளின் எண்ணிக்கையும் நாட்களின் எண்ணிக்கையும்எதிர் விகிதத்தில் உள்ளன.
\(x\) மற்றும் \(y\) அளவுகள் எதிா் விகிதத்தில் இருக்கும்போது, நாம் \(=\) அல்லது \(=\) என்று எழுதலாம். , என்பது \(x\)ன் , மதிப்புகளுடன் தொடா்புடைய \(y\)ன் மதிப்புகள் .
, என்பன \(y\)ன் மதிப்புகள் மற்றும் , என்பன அதனோடு தொடா்புடைய \(x\)ன் மதிப்புகள்.
, என்பன \(y\)ன் மதிப்புகள் மற்றும் , என்பன அதனோடு தொடா்புடைய \(x\)ன் மதிப்புகள்.
அறியப்பட்ட மதிப்புகளை மாற்றவும்.
\(\frac {20}{30}\) \(=\) \(\frac{x}{6}\)
\(\frac {2}{3}\) \(=\) \(\frac{x}{6}\)
\(3\) \(×\) \(x\) \(=\) \(2\) \(×\) \(6\)
\(3x =\) \(12\)
\(x =\) \(\frac{12}{3}\)
\(x =\)\(4\)
எனவே, உணவு நான்கு நாட்களுக்கு நீடிக்கும்.
Register for free to see more content