PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசர்வசம கொள்கையை நம்மை சுற்றி உள்ள பொருகளின் மூலம் அறியலாம்.
எனவே, இது வடிவியல் வடிவங்களில் உள்ளது என்பது பொருட்டல்ல.
சில சர்வசமங்களை பற்றி பார்க்கலாம்.
1. சர்வசம கோடுகள்
2. சர்வசம கோணங்கள்
3. சர்வசம வட்டங்கள்
4. சர்வசம பலகோணங்கள்
மேற்கண்டவற்றை சற்று விரவாக காணலாம்.
சர்வசம கோடுகள்
ஒரே நீளமுடைய இரு கோடுகள் சர்வசம கோடுகள் என்றழைக்கப்படுகின்றன. ஆனால் கோடுகளின் நிலைகள் மற்றும் கோணங்கள் சமமாக இருக்க வேண்டிய அவசியம் இல்லை.
Example:
இங்கு, கோட்டுத்துண்டு \(\overline{AB}\) மற்றும் \(\overline{CD}\) ஆகியவை ஒரே நீளம் உடையவை. எனவே, இவை சர்வசம கோடுகள் ஆகும். இதனை, \(\overline{AB}\) \(\overline{CD}\) என எழுதலாம்.
சர்வசம கோணங்கள்
சர்வசமக் கோணங்கள் அவற்றின் கோண அளவை மட்டுமே சார்ந்தவை. கதிர்களின்
நீளங்களைச் சார்ந்தவை அல்ல. எனவே, இரு கோணங்களின் கோண அளவுகள் சமம் எனில்,
அவை சர்வசமக் கோணங்கள் என அழைக்கப்படும்.
Example:
இங்கு, \(∠R\)மற்றும் \(∠Q\) கோணம் \(x°\) ஆகும். எனவே, \(∠R\) மற்றும் \(∠S\) சர்வசம கோணங்கள். இதனை குறியீட்டில் \(∠R\)\(∠Q\) என எழுதலாம்.
சர்வசம வட்டங்கள்
ஒரே அளவு ஆரம், விட்டம் சுற்றளவு கொண்ட இரு வட்டங்கள் சர்வசம வட்டங்கள் ஆகும். அவை ஒன்றின் மீது ஒன்று
முழுவதுமாகப் பொருந்தும்.
Example:
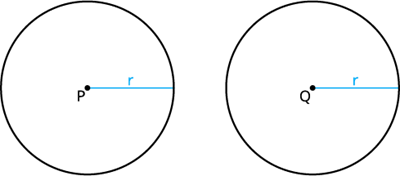
இங்கு, இரு வட்டங்கள் \(P\) மற்றும் \(Q\) ஆகியவை ஒரே ஆரம் \(r\) கொண்டவை . எனவே, வட்டம் \(P\) மற்றும் \(Q\) ஆகியன சர்வ சம வட்டங்கள் ஆகும்.
சர்வசம பலகோணங்கள்
சம எண்ணிக்கையிலான பக்கங்களைக் கொண்ட இரண்டு பலகோணங்களின் பக்கங்கள் மற்றும் கோணங்கள் சர்வசம் எனில் இரு பல கோணங்களும் சர்வசம பலகோணங்கள் என்று அழைக்கப்படுகின்றன.
Example:
இங்கு, பல்கோணம் \(ABCDE\) மற்றும் \(PQRST\) ஆகியவை \(5\) பக்கங்கள் கொண்டுள்ளன, மேலும் \(AB = PQ\), \(BC = QR\), \(CD = RS\), \(DE = ST\), \(EA = TP\), \(∠A = ∠P\), \(∠B = ∠Q\), \(∠C = ∠R\), \(∠D = ∠S\) மற்றும் \(∠E = ∠T\).
எனவே, \(ABCDE\) மற்றும் \(PQRST\) ஆகியவை சர்வசம பல கோணம் ஆகும். அதாவது, \(ABCDE\) \(PQRST\).
Register for free to see more content