PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஒரே வட்டத்துண்டில் அமையும் கோணங்கள்:
கற்பனையாக:
வட்டத்தின் மையம் O மற்றும் நாண் PQ.
R மற்றும் S என்பன ஒரே வட்டத்துண்டில் வட்டத்தில் மேல் அமையும் புள்ளிகள் ஆகும்.
நாணின் PQ முனைகளை மையம் O வுடன் இணைக்க.
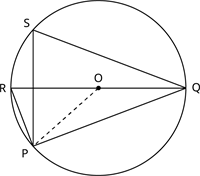
ஒரு வட்டவில் மையத்தில் தாங்கும் கோணம் அந்த வில்லை தவிர்த்து வட்டத்தின் மீதிப் பரிதியில் ஏதேனும் ஒரு புள்ளியில் ஏற்படுத்தும் கோணத்தைப் போல் இரு மடங்காகும்.
\frac{1}{2} \angle POQ = \angle PRQ …… \text{சமன்பாடு}(1)
இதேபோன்று, \frac{1}{2} \angle POQ = \angle PSQ …… \text{சமன்பாடு}(2)
(1) மற்றும் (2) இல் இருந்து:
\angle PRQ = \angle PSQ
தேற்றம் : ஒர் வட்டத்துண்டில் அமையும் கோணங்கள் சமம்.
விளக்கம்:
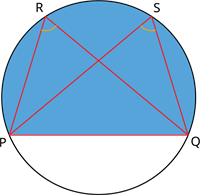
தேற்றத்தின் படி, ஒர் வட்டத்துண்டில் அமையும் கோணங்கள் சமம். வட்டத்தின் கோணங்கள் \angle PRQ மற்றும் \angle PSQ சமம் மற்றும் ஒரே கோட்டுத் துண்டில் அமைந்துள்ளது. (i.e.) \angle PRQ = \angle PSQ.
Example:
கோணங்கள் x மற்றும் y காண்க படத்தில் இருந்து, O என்பது மையமாகும்.
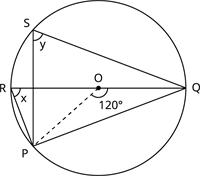
விடை:
தேற்றத்தின் படி, ஒரு வட்டவில் மையத்தில் தாங்கும் கோணம் அந்த வில்லை தவிர்த்து வட்டத்தின மீதிப் பரிதியில் ஏதேனும் ஒரு புள்ளியில் ஏற்படுத்தும் கோணத்தைப் போல் இரு மடங்காகும்.
இதுவே:
\angle PRQ = \frac{1}{2} \angle POQ
x = \frac{1}{2} \மடங்கு 120^{\circ}
= 60^{\circ}
மேலும், தேற்றத்தின் படி, ஒர் வட்டத்துண்டில் அமையும் கோணங்கள் சமம்.
எனவே, \angle PRQ = \angle PSQ.
ஆகவே, x = y.
y = 60^{\circ}.
Important!
தேற்றத்தின் மறுதலை:
Important!
ஒரு கோட்டுத்துண்டில் இரு புள்ளிகளை இணைப்பதால் உண்டாகும் கோணம் அதே பக்கத்தில் மற்றொரு கோட்டுத்துண்டினை இணைப்பதால் உண்டாகும் கோணமும் சமம். நான்கு
புள்ளிகளும் வட்டத்தின் மேற்பரப்பில் உள்ளது.
விளக்கம்:
தேற்றத்தின் படி, கோட்டுதுண்டு PQ ஏற்படுத்தும் கோணம் R மற்றும் S அதே பக்கத்தில்
மற்றொரு கோட்டுத்துண்டானது PQ ஏற்படுத்தும் கோணங்கள் P, Q, R மற்றும் S வட்டத்தின் மீது உள்ளது.
Register for free to see more content