PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoMixed fractions contain a whole number and a proper fraction. They can also be represented as an improper fraction.
Example:
; where \(3\) is a whole number and \(4/5\) is a proper fraction.
Converting mixed fraction to improper fraction: To convert a mixed fraction to improper fraction, the following steps are to be followed.
Step 1: Multiply the denominator of the proper fraction and whole number and add it with the numerator of the fraction to get the numerator of the improper fraction.
Step 2: Denominator of an improper fraction is the same as the denominator of a mixed fraction.
Example:
Convert to an improper fraction.
Step 1: Numerator of improper fraction \(=\) (denominator of the proper fraction \(×\) whole number) \(+\) numerator of a proper fraction.
\(= 5 × 3 = 15 + 4 = 19\).
Step 2: Denominator of improper fraction \(=\) denominator of the mixed fraction.
The denominator of improper fraction \(= 5\).
Improper fraction \(= 19 / 5\).
Thus, \(= 19 / 5\).
Converting improper fraction to mixed fraction: To convert the improper fraction to mixed fraction, the following steps are to be followed.
Divide the given fraction to find quotient and remainder.
The whole number in mixed fraction \(=\) quotient of division.
The numerator of mixed fraction \(=\) remainder of a division.
The denominator of mixed fraction \(=\) denominator of the improper fraction.
Example:
Convert \(15/4\) to a mixed fraction.
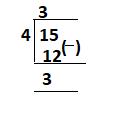
The remainder is \(3\), the quotient is \(3\).
The whole number in mixed fraction \(=\) quotient of division \(= 3\).
The numerator of mixed fraction \(=\) reminder of division \(= 3\).
The denominator of mixed fraction \(=\) denominator of improper fraction \(= 4\).
Thus, \(15/4 =\) .
Register for free to see more content