
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAn equation in which three variables \(x\), \(y\) and \(z\) is of the first degree, then the equation is said to be a linear equation in three variables.
The general form of linear equation in three variables can be written as:
\(ax + by + cz + d = 0\)
Here, at least one of \(a\), \(b\), \(c\) and \(d\) are non-zero, and they are real numbers, and \(x\) and \(y\) are variables.
Graphical representation
A linear equation in two variables is of the form \(ax + by + c = 0\) and represents a straight line.
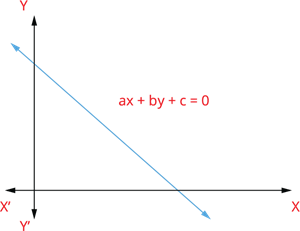
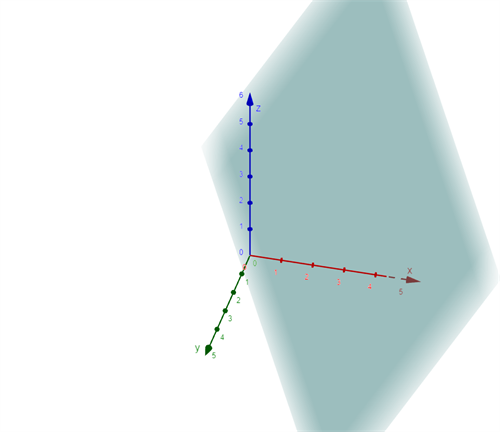
A linear equation in three variables is of the form \(ax + by + cz + d = 0\) is a plane.
Solution of the system of equations
The general form of a system of linear equations in three variables is given by:
\(a_1x + b_1y + c_1z + d_1 = 0\)
\(a_2x + b_2y + c_2z + d_2 = 0\)
\(a_3x + b_3y + c_3z + d_3 = 0\)
Exactly one solution: Three equations meet at a common point in a plane, and then the system of equations has only one solution.

Infinitely many solutions: If three equations lie on the same plane, then the system of equations has infinitely many solutions.

No solution: Three equations do not have any common point.

Steps to solve the system of linear equations in three variables
Step 1: Consider any \(2\) equations from \(3\) equations. Multiply the equations with suitable values such that any one of the variables gets cancelled, leaving the variables either \(x\) and \(y\) or \(x\) and \(z\) or \(y\) and \(z\).
Step 2: Again, consider any \(2\) equations from \(3\) equations and eliminate the same variable which was eliminated in the previous pair.
Step 3: Now, we have \(2\) equations with two variables.
Step 4: Solve these \(2\) equations using any method like substitution or elimination or cross multiplication method.
Step 5: Substitute the value of these \(2\) variables in any of the given equations and determine the value of the third variable.
Important!
1. In any of the steps, the system is inconsistent and has no solution if we get a false equation like \(0 = 1\),
2. If we get an equation like \(0 = 0\), the system is consistent and has infinitely many solutions.