PDF chapter test TRY NOW

10. Construction of a tangent to a circle using alternate segment theorem

Working rule to construct a tangent to a circle (Using Alternate Segment Theorem):

Given the radius of a circle, let us learn how to construct a tangent to the circle using its alternate segment theorem.

Example:

Draw a circle of radius

$4$

$cm$ . Then, at a point

$L$ on it, draw a tangent to the circle using the alternate segment.

Rough Sketch:

Construction:

Step $1$ : With

$O$ as the centre, draw a circle of radius

$4$

$cm$ .

Step $2$ : Take a point

$L$ on the circle. Through

$L$ , draw any chord

$LM$ .

Step $3$ : Take two points

$M$ and

$N$ distinct from

$L$ on the circle, so that

$L$ ,

$M$ and

$N$ are in anti-clockwise direction. Join

$LN$ and

$NM$ .

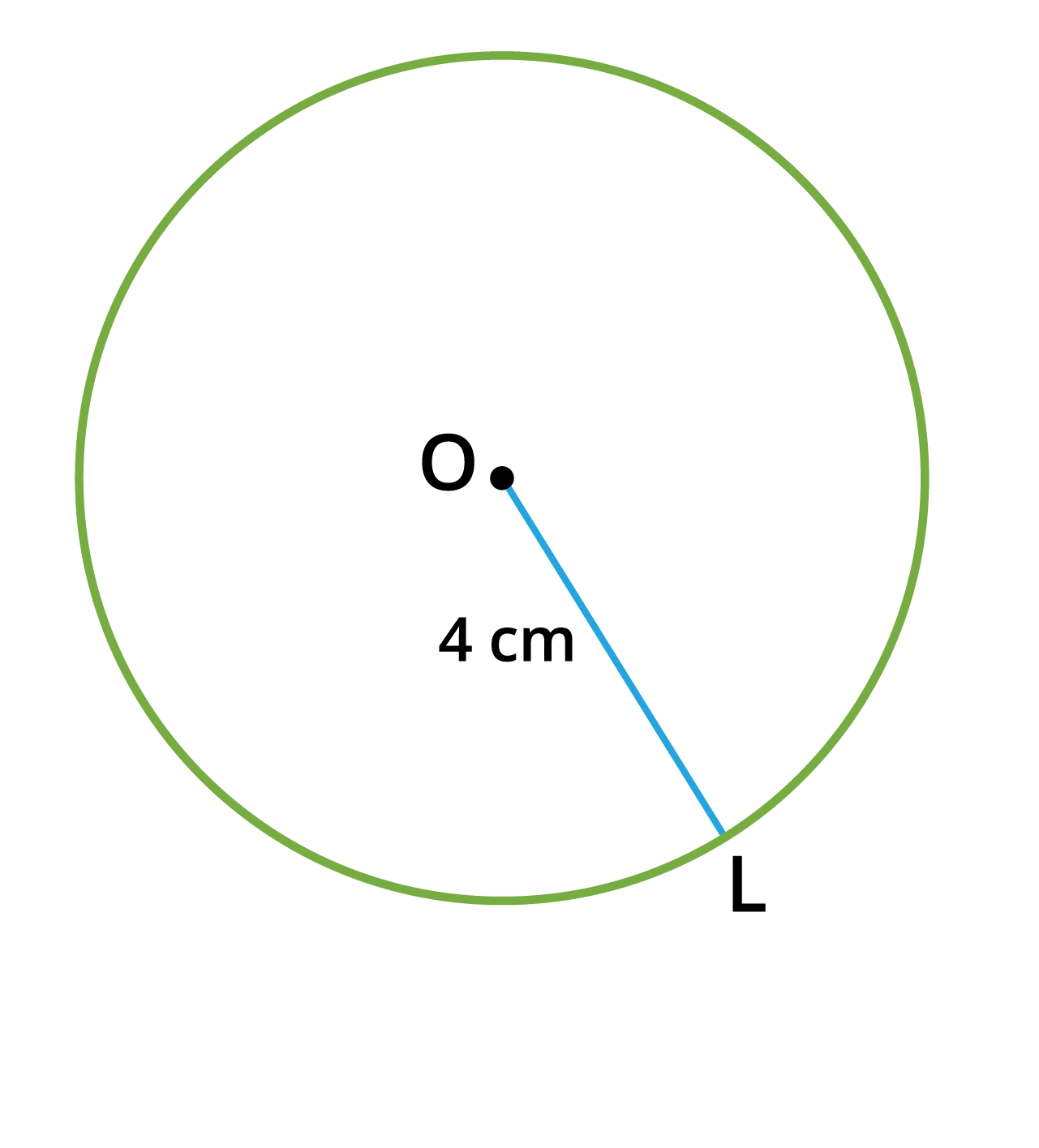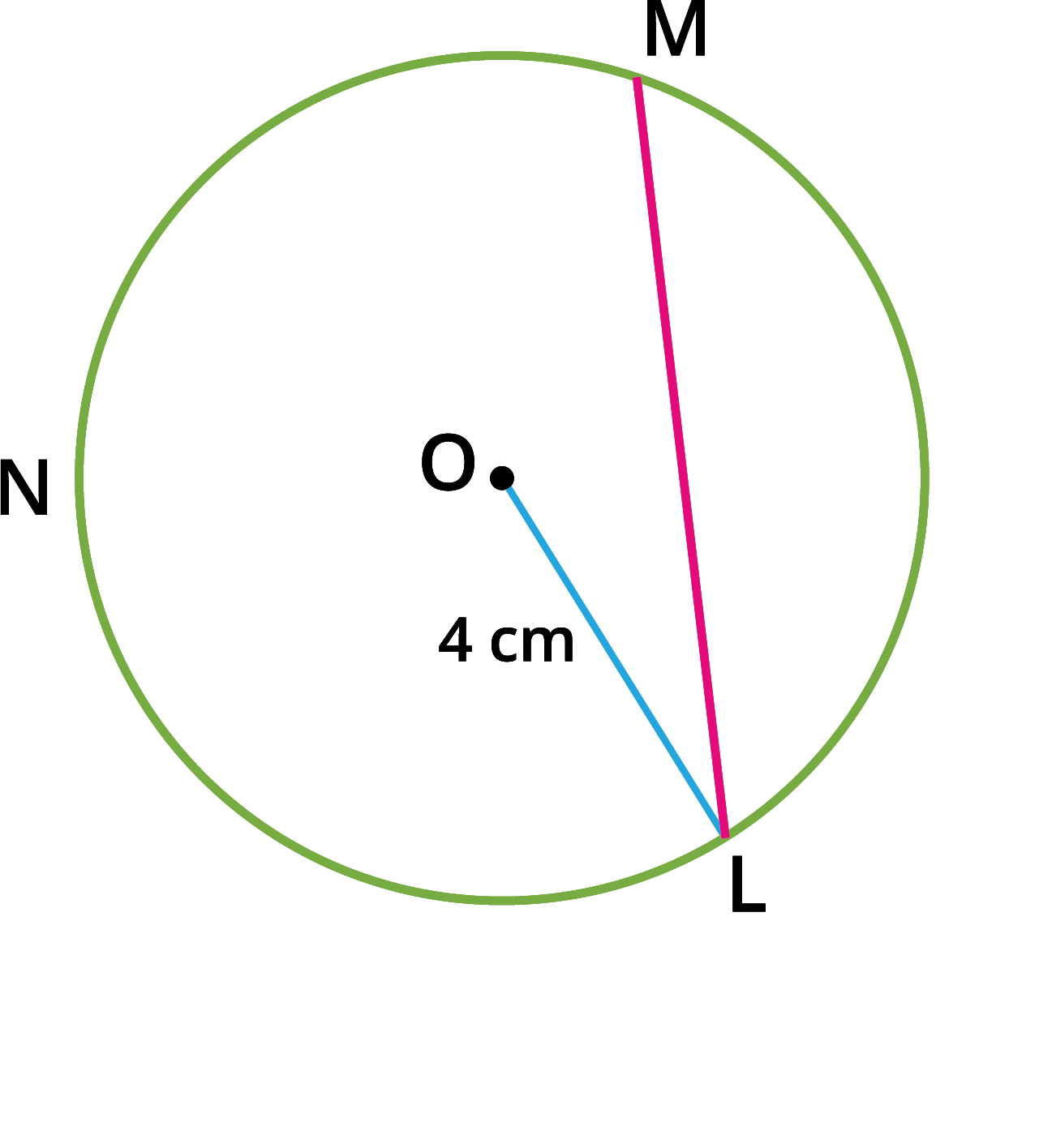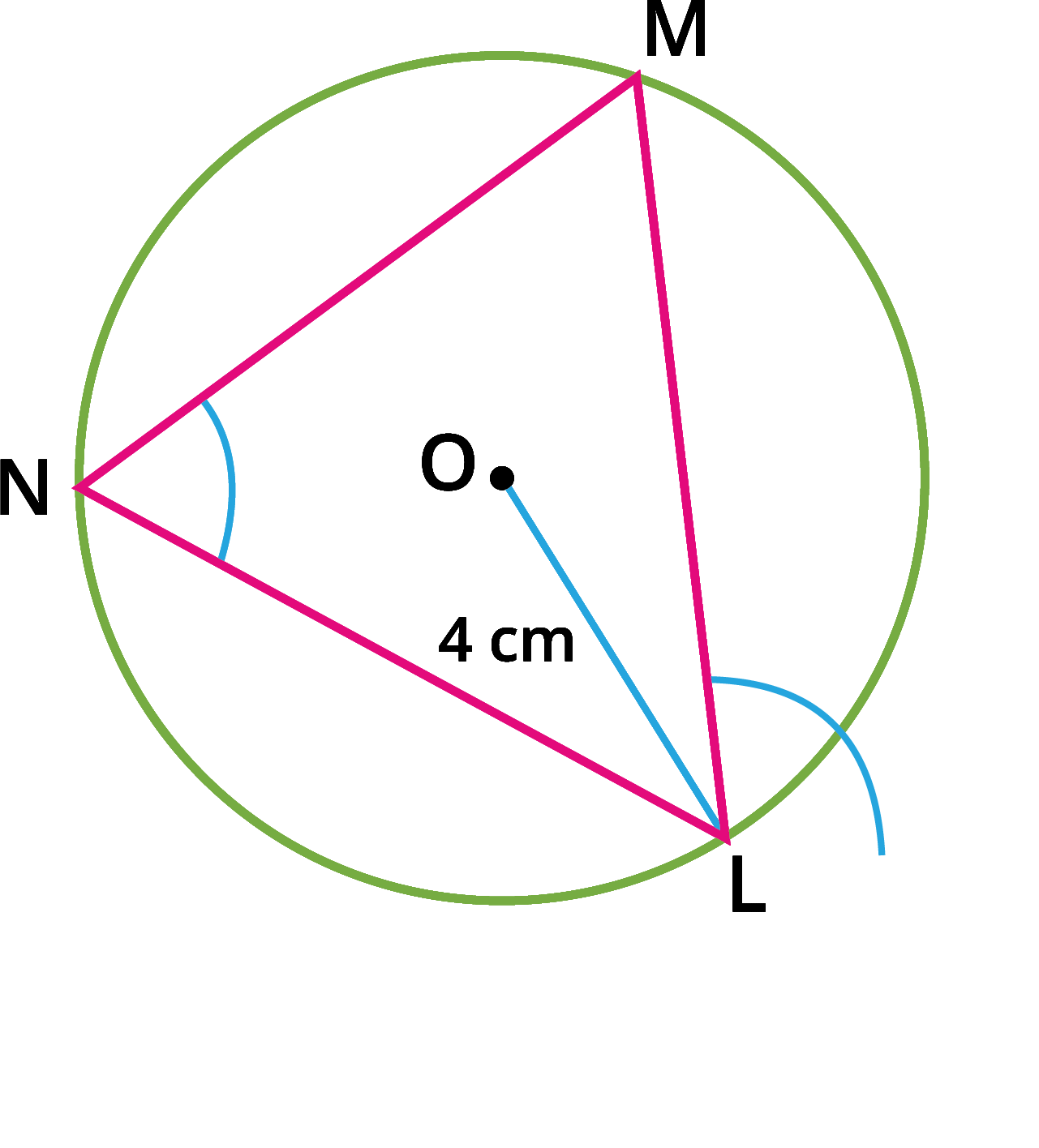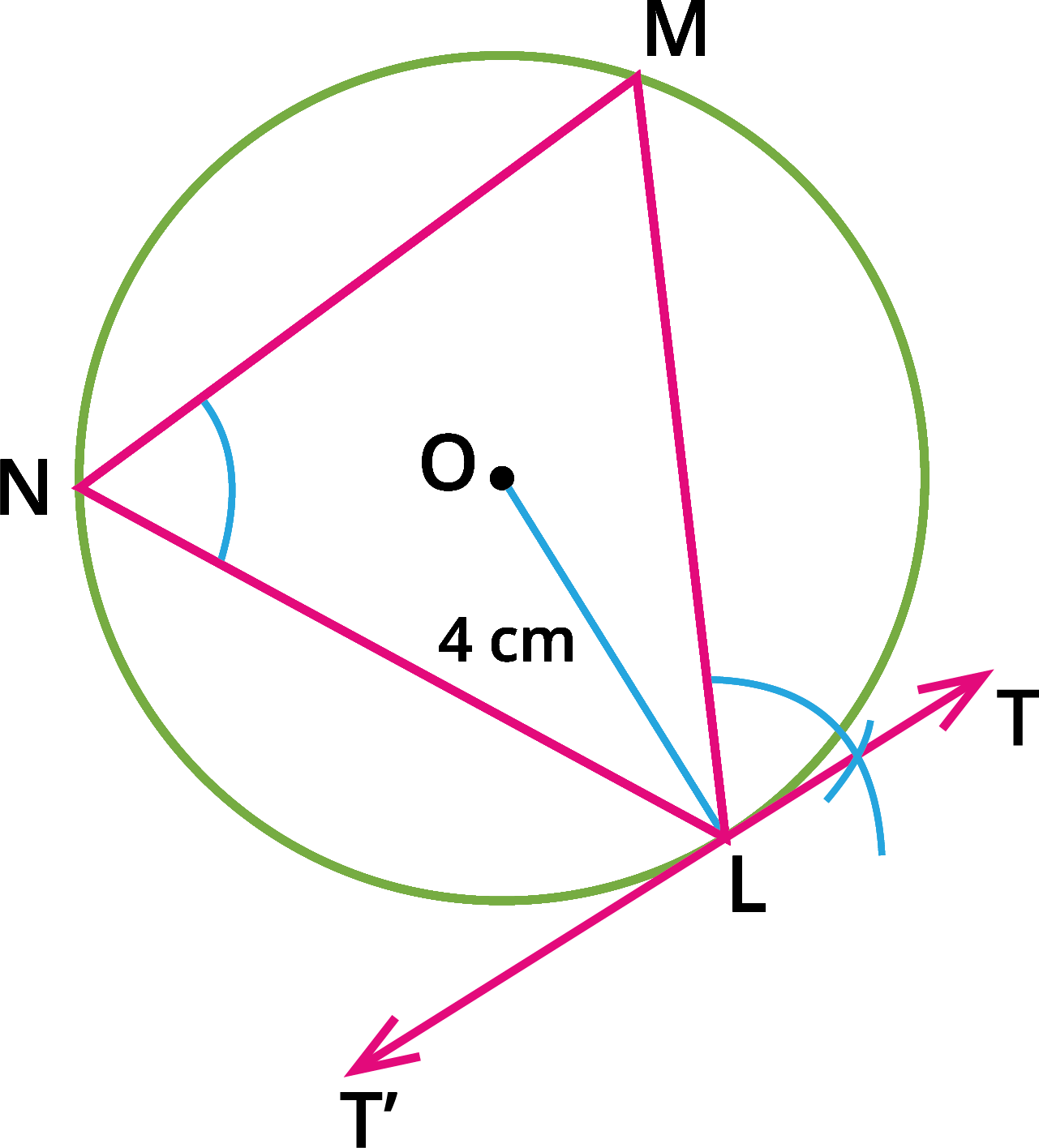
Step $4$ : Through

$L$ draw a tangent

$TT'$ such that

$\angle TLM$

$=$

$\angle MNL$ .

Step $5$ :

$TT'$ is the required tangent.

Did you find an error?