11. Construction of a pair of tangents to a circle from an external point

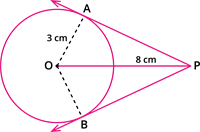
Draw a circle of diameter \(6\) \(cm\) from a point \(P\), which is \(8\) \(cm\) away from its centre. Draw the two tangents \(PA\) and \(PB\) to the circle and measure their lengths.

 

Given:

 

The diameter of the circle \(=\) \(6\) \(cm\).

Radius \(=\) \(\frac{6}{2}\)

 

\(=\) \(3\) \(cm\)

 

Rough Sketch:

 

 

Construction:

 

Step \(1\): With \(O\) as the centre, draw a circle of radius \(3\) \(cm\).

 

Step \(2\): Draw a line \(OP\) of length \(8\) \(cm\).

 

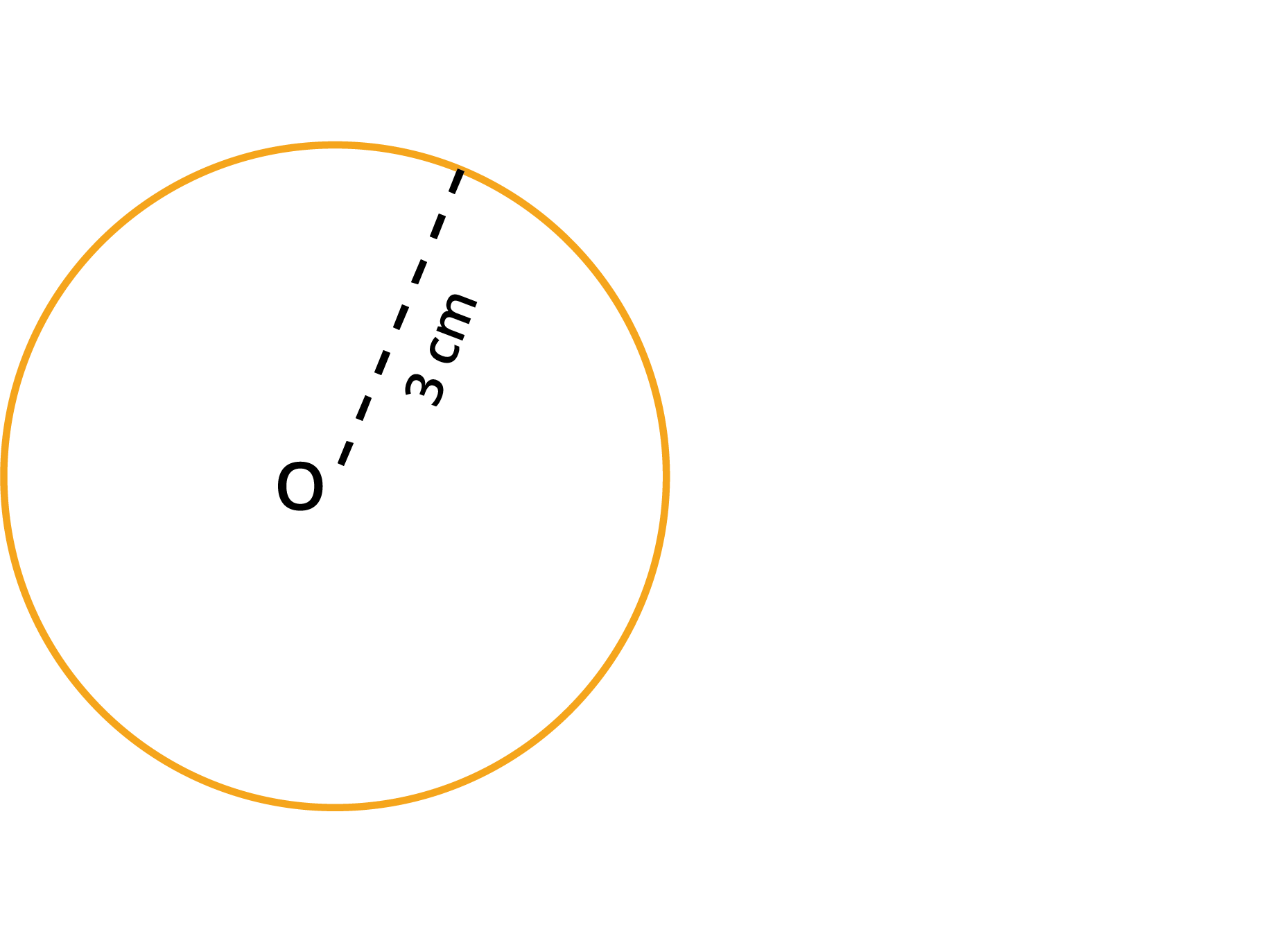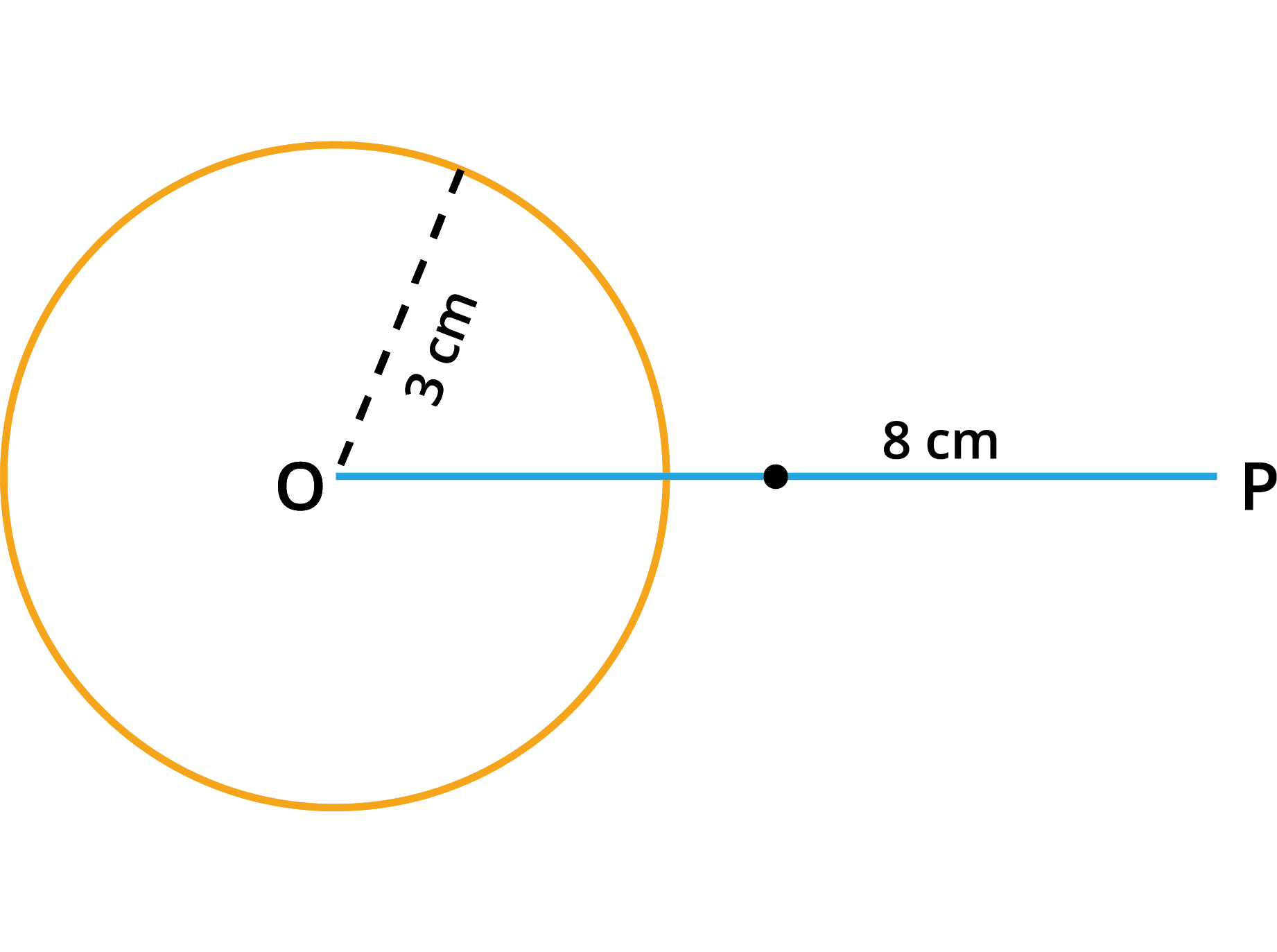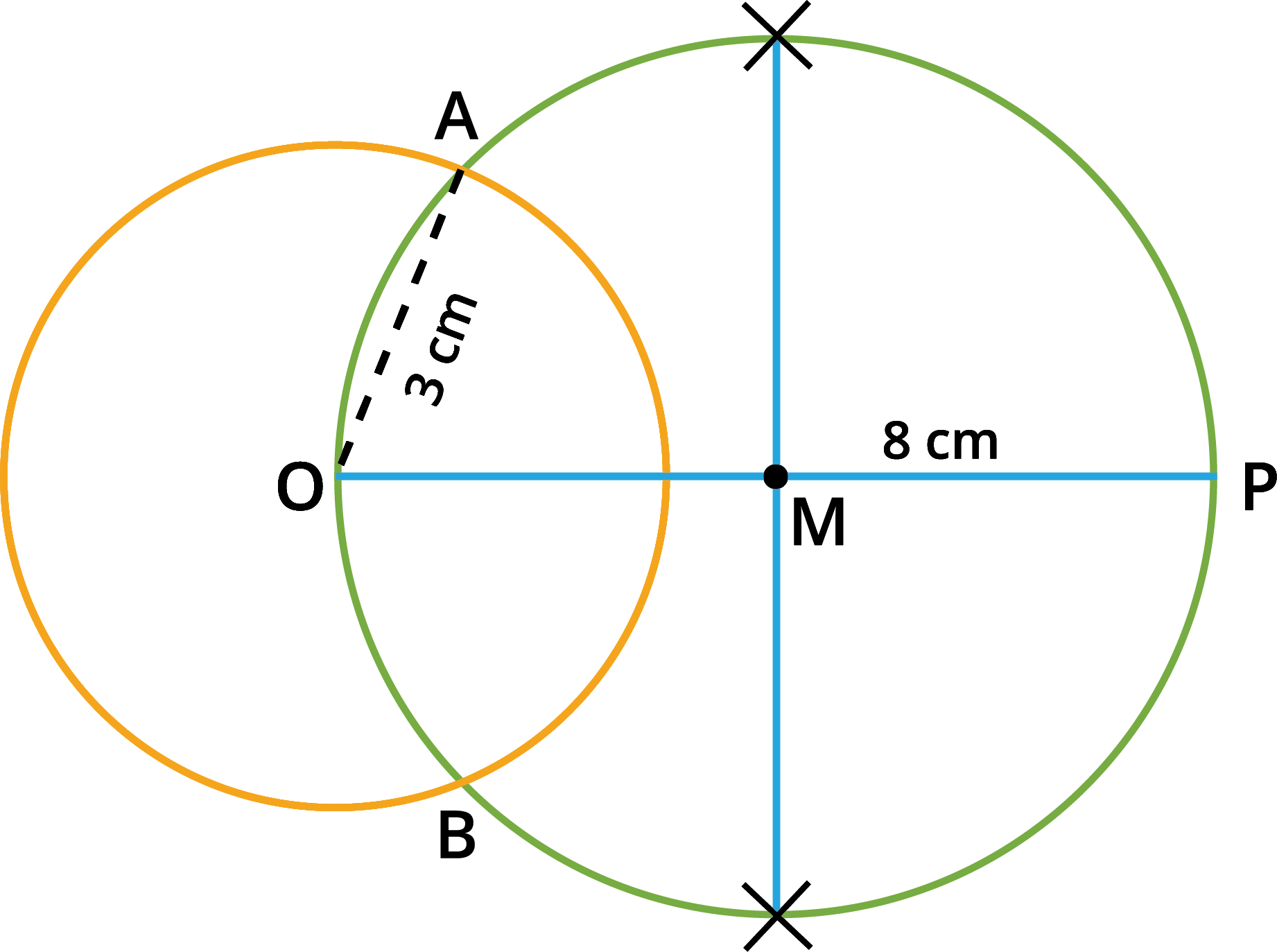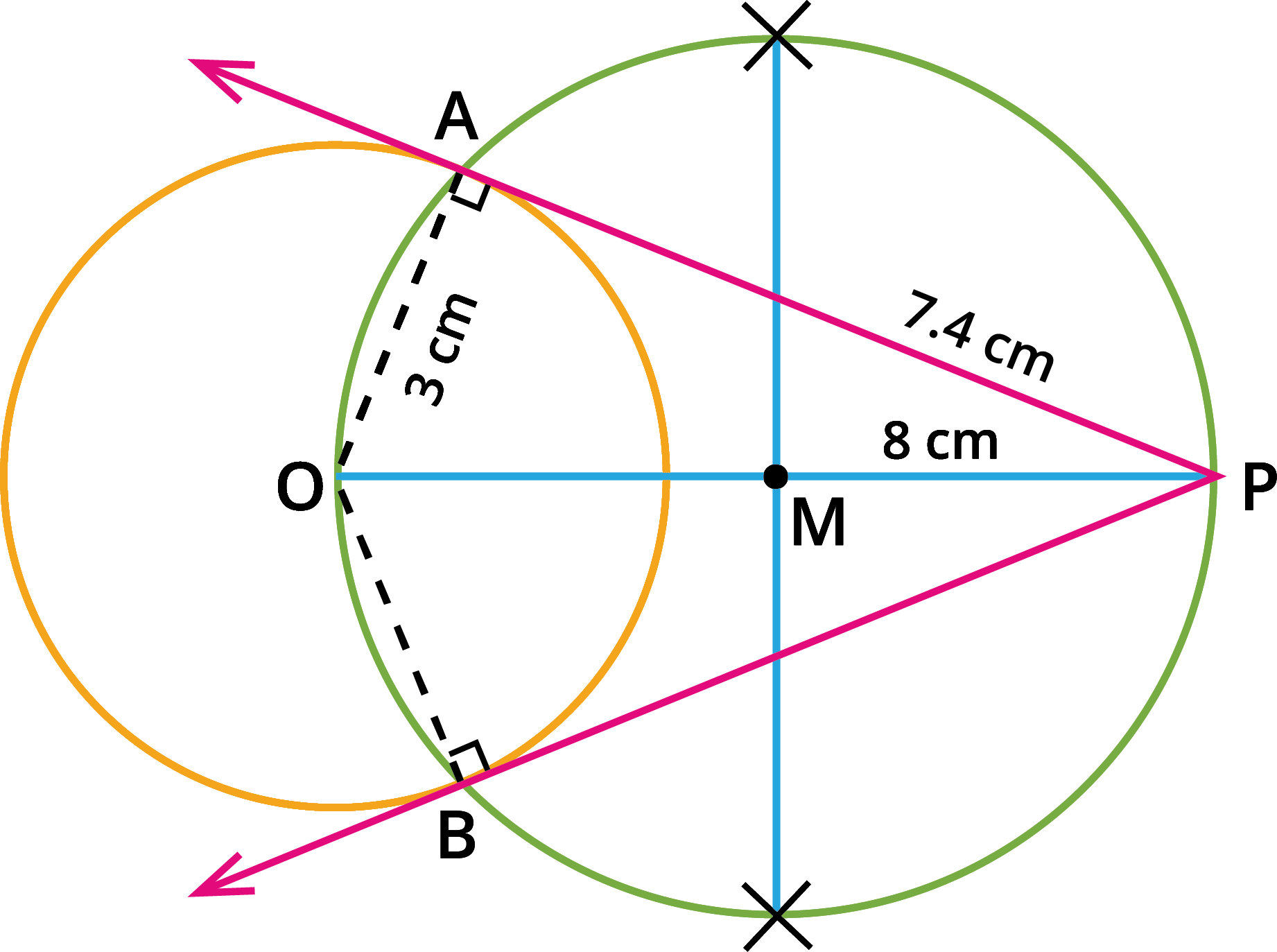
Step \(3\): Draw a perpendicular bisector of \(OP\), which cuts \(OP\) at \(M\).

 

Step \(4\): With \(M\) as the centre and \(MO\) as the radius, draw a circle that cuts the previous circle at \(A\) and \(B\).

 

Step \(5\): Join \(AP\) and \(BP\). \(AP\) and \(BP\) are the required tangents. Thus the length of the
tangents are \(PA = PB = 7.4\) \(cm\).

 

Verification:

 

In the right angle triangle \(OAP\) by the Pythagoras theorem, we have:

 

\(OP^2\) \(=\) \(OA^2\) \(+\) \(PA^2\)

 

\(\Rightarrow\) \(PA^2\) \(=\) \(OP^2\) \(-\) \(OA^2\)

 

\(PA^2\) \(=\) \(8^2\) \(+\) \(3^2\)

 

\(PA^2\) \(=\) \(64 – 9\)

 

\(PA^2\) \(=\) \(55\)

 

\(\Rightarrow PA = \sqrt{55}\)

 

\(PA\) \(=\) \(7.4\) \(cm\) (approximately) .