PDF chapter test TRY NOW
Cevian:
A cevian is a line segment that extends from one vertex of a triangle to the opposite side.
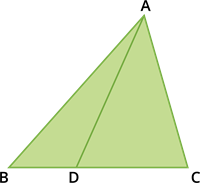 |
In the figure, \(AD\) is a cevian from \(A\).
Special Cevians of a Triangle:
- A median is a cevian that divides the opposite side into two equal lengths.
- An altitude is a cevian that is perpendicular to the opposite side.
- An angle bisector is a cevian that bisects the corresponding angle.
Ceva’s Theorem (without proof):
Let \(ABC\) be a triangle and let \(D\), \(E\), \(F\) be points on lines \(BC\), \(CA\) and \(AB\) respectively.
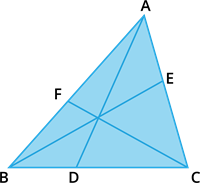 |
Then the cevians \(AD\), \(BE\), \(CF\) are concurrent if and only if \(\frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB} = 1\) where the lengths are directed. This also works for the reciprocal of each of the ratios as the reciprocal of \(1\) is \(1\).
Example:
The cevians \(AD\), \(BE\) and \(CF\) of the triangle \(ABC\) are congruent. If \(\frac{BD}{DC} = \frac{2}{5}\), \(\frac{CE}{EA} = \frac{3}{4}\) and \(\frac{AF}{FB} = \frac{x}{6}\), find the value of \(x\).
Solution:
By Ceva's theorem, we have \(\frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB} = 1\).
Substitute the required values in the above equation.
\(\Rightarrow\) \(\frac{2}{5} \times \frac{3}{4} \times \frac{x}{6} = 1\)
\(\Rightarrow\) \(x\) \(=\) \(1 \times \frac{5}{2} \times \frac{4}{3} \times 6\)
\(\Rightarrow\) \(x\) \(=\) \(20\)
Menelaus Theorem (without proof):
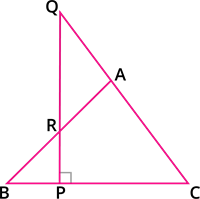 |
A necessary and sufficient condition for points \(P\), \(Q\), \(R\) on the respective sides \(BC\), \(CA\), \(AB\) (or their extension) of a triangle \(ABC\) to be collinear is that \(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = -1\) where all segments in the formula are directed segments.
Important!
- Menelaus theorem is also given by \(BP \times CQ \times AR = − PC \times QA \times RB\).
- If any one of the six directed line segments \(BP\), \(PC\), \(CQ\), \(QA\), \(AR\), or \(RB\) is interchanged, then the product will be \(1\).
Example:
On a random board, three pins \(P\), \(Q\), \(R\) are punched in the way, \(BP = 3\) \(cm\), \(CQ = 4\) \(cm\), \(RA = 5\) \(cm\), \(PC = 2\) \(cm\), \(QA = 5\) \(cm\), \(RB = 6\) \(cm\), where \(A\), \(B\) and \(C\) are points such that \(P\) lies on \(BC\), \(Q\) lies on \(AC\) and \(R\) lies on \(AB\). Check whether the pins \(P\), \(Q\) and \(R\) lie on the same straight line.
Solution:
Note that the directed segment \(AR\) is interchanged as \(RA\).
By Menelaus theorem, the pins \(P\), \(Q\) and \(R\) will lie on the same straight line if BP
\(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = 1\).
\(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = 1\).
Consider the left-hand side of the equation.
\(\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB}\)
Substitute the required values in the above equation.
\(=\) \(\frac{3}{2} \times \frac{4}{5} \times \frac{5}{6}\)
\(=\) \(\frac{60}{60}\)
\(=\) \(1\)
Therefore, the pins \(P\), \(Q\) and \(R\) lie on the same straight line.
