UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreResult \(6\):
The two direct common tangents drawn to the circles are equal in length.
Explanation:
 |
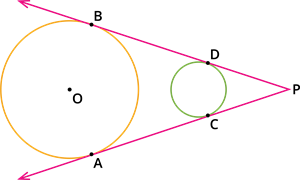The two direct common tangents \(AC\) and \(BD\) from \(P\) drawn to the circles are equal in length.
\(\Rightarrow\) \(AC\) \(=\) \(BD\)
Proof of the result:
By the result \(3\), we have:
The lengths of the two tangents drawn from an exterior point to a circle are equal.
\(PA\) \(=\) \(PB\) and \(PC\) \(=\) \(PD\).
Subtract the above two equations.
\(PA\) \(-\) \(PC\) \(=\) \(PB\) \(-\) \(PD\)
\(AC\) \(=\) \(BD\)
Example:
In the above given figure if \(PB\) \(=\) \(9\) \(cm\) and \(AC\) \(=\) \(6\) \(cm\), find the length of the tangent \(PD\).
Solution:
By the result, we know that \(AC\) \(=\) \(BD\).
So, \(BD\) \(=\) \(6\) \(cm\).
From the figure it is observed that, \(PD\) \(=\) \(PB\) \(-\) \(BD\).
\(PD\) \(=\) \(9\) \(cm\) \(-\) \(6\) \(cm\)
\(PD\) \(=\) \(3\) \(cm\)
Therefore, the length of the tangent \(PD\) \(=\) \(3\) \(cm\).
Register for free to see more content