PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoStatement:
If a line touches a circle and from the point of contact a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.
Explanation:
 |
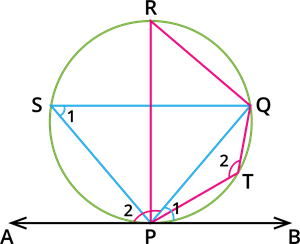In the figure, the chord \(PQ\) divides the circle into two segments. Then, the tangent \(AB\) is drawn such that it touches the circle at \(P\).
Thus, the angle in the alternate segment for \(\angle QPB\) is \(\angle QSP\) and that for \(\angle QPA\) is \(\angle PTQ\) are equal.
Then, \(\angle QPB\) \(=\) \(\angle QSP\) and \(\angle QPA\) \(=\) \(\angle PTQ\).
Proof for the theorem:
Given:
Let \(O\) be the centre of the circle.
The tangent \(AB\) touches the circle at \(P\), and \(PQ\) is a chord.
Let \(S\) and \(T\) be the two points on the circle on the opposite sides of chord \(PQ\).
To prove:
(i) \(\angle QPB\) \(=\) \(\angle QSP\) and
(ii) \(\angle QPA\) \(=\) \(\angle PTQ\)
Construction:
Draw the diameter \(POR\) and draw \(QR\), \(QS\) and \(PS\).
Proof:
 |
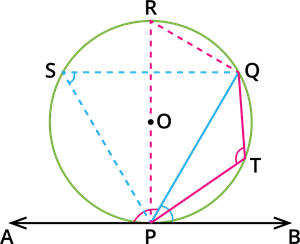The diameter \(RP\) is perpendicular to the tangent \(AB\).
So, \(\angle RPB\) \(=\) \(90^{\circ}\).
\(\Rightarrow\) \(\angle RPQ\) \(+\) \(\angle QPB\) \(=\) \(90^{\circ}\) …… \((1)\)
Consider the triangle \(RPQ\).
We know that:
Angle in a semicircle is \(90^{\circ}\).
By the theorem, we have \(\angle RQP\) \(=\) \(90^{\circ}\). …… \((2)\)
Thus, \(RPQ\) is a right-angled triangle.
The sum of the two acute angles in the right-angled triangle, is \(90^{\circ}\).
\(\Rightarrow\) \(\angle QRP\) \(+\) \(\angle RPQ\) \(=\) \(90^{\circ}\) …… \((3)\)
From equations \((1)\) and \((3)\), we have:
\(\angle RPQ\) \(+\) \(\angle QPB\) \(=\) \(\angle QRP\) \(+\) \(\angle RPQ\)
\(\Rightarrow\) \(\angle QPB\) \(=\) \(\angle QRP\) …… \((4)\)
We know that:
Angles in the same segment are equal.
By the theorem, we have \(\angle QRP\) \(=\) \(\angle PSQ\). …… \((5)\)
From equations \((4)\) and \((5)\), we have:
\(\angle QPB\) \(=\) \(\angle PSQ\). …… \((6)\)
Therefore, statement (i) is proved.
It is observed that \(\angle QPA\) and \(\angle QPB\) are linear angles.
We know that:
The linear pair of angle are always supplementary.
\(\Rightarrow\) \(\angle QPA\) \(+\) \(\angle QPB\) \(=\) \(180^{\circ}\) …… \((7)\)
Consider the cyclic quadrilateral \(PSQT\).
By the theorem, we have:
The sum of opposite angles of a cyclic quadrilateral is \(180^{\circ}\).
\(\angle PSQ\) \(+\) \(\angle PTQ\) \(=\) \(180^{\circ}\). …… \((8)\)
From equations \((7)\) and \((8)\), we have:
\(\angle QPA\) \(+\) \(\angle QPB\) \(=\) \(\angle PSQ\) \(+\) \(\angle PTQ\)
Substitute equation \((6)\) in the above equation.
\(\Rightarrow\) \(\angle QPA\) \(+\) \(\angle QPB\) \(=\) \(\angle QPB\) \(+\) \(\angle PTQ\)
\(\Rightarrow\) \(\angle QPA\) \(=\) \(\angle PTQ\)
Therefore, statement (ii) is proved.
Example:
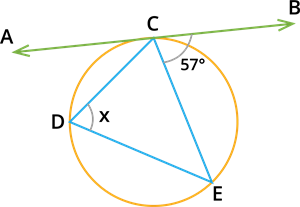
In the figure, \(AB\) is the tangent, and \(CF\) is the chord of the given circle. Next, find the value of \(x\).
Solution:
Given, \(\angle BCF\) \(=\) \(57^{\circ}\).
By the Alternate Segment Theorem, \(\angle BCF\) \(=\) \(\angle CDE\).
Thus, \(x\) \(=\) \(57^{\circ}\).
Therefore, the value of \(x\) \(=\) \(57^{\circ}\).
Important!
This theorem is also known as Tangent - chord theorem.
Register for free to see more content