PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoStatement:
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Explanation:
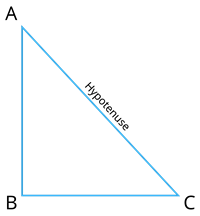
In the triangle \(ABC\), if \(AC^2 = AB^2 + BC^2\) then, the angle opposite to the side \(AC\) is the right angle.
That is, \(\angle B = 90^{\circ}\).
Proof of the theorem:
Given:
A triangle \(ABC\) such that \(AC^2 = AB^2 + BC^2\).
To prove:
\(\angle B = 90^{\circ}\)
Proof:
Construct a triangle \(LMN\) right angled at \(M\) such that:
\(LM\) \(=\) \(AB\) \(…… (1)\)
\(MN\) \(=\) \(BC\) \(…… (2)\)
By the Pythagoras theorem, we have \(LN^2 = LM^2 + MN^2\).
By the construction we have \(LN^2 = AB^2 + BC^2\) \(…… (3)\)
Given that, \(AC^2 = AB^2 + BC^2\) \(…… (4)\)
On comparing equations \((1)\) and \((2)\) we have, \(LN^2\) \(=\) \(AC^2\).
\(\Rightarrow\) \(LN\) \(=\) \(AC\) \(…… (5)\)
Thus, from the equations \((1)\), \((2)\) and \((3)\) we say that \(\Delta ABC\) \(\cong\) \(\Delta LMN\).
By the CPCT theorem (If two or more triangles which are congruent to each other are taken, then the corresponding angles and the sides of the triangles are also congruent to each other.), we have:
\(\angle B\) \(=\) \(\angle M\).
By the construction we have \(\angle M = 90^{\circ}\).
Therefore, \(\angle B = 90^{\circ}\).
Hence, the proof.
Example:
If the triangle is with dimensions \(10\) units, \(8\) units, and \(6\) units, then show that it is a right-angled triangle.
Proof:
Let \(ABC\) be the given triangle.
Then, \(AC\) \(=\) \(10\) units, \(AB\) \(=\) \(6\) units and \(BC\) \(=\) \(8\) units.
Let us verify whether \(AC^2 = AB^2 + BC^2\).
\(10^2\) \(=\) \(6^2\) \(+\) \(8^2\)
\(100\) \(=\) \(36 + 64\)
\(100\) \(=\) \(100\)
The left-hand side and the right-hand side value are equal.
Hence, \(AC^2 = AB^2 + BC^2\).
By the converse of the Pythagoras theorem, it is evident that the triangle \(ABC\) is right-angled at \(B\).
That is, \(B\) \(=\) \(90^{\circ}\).
Therefore, the triangle with dimensions \(10\) units, \(8\) units and \(6\) units is a right angled triangle.
Important!
(i) The three positive integers \(x\), \(y\) and \(z\) which satisfies the Pythagorean theorem are called Pythagorean triplets.
Example:
(ii) If \(l\) is any positive integer and \((x, y, z)\) is a Pythagorean triplet, then \((lx, ly, kz)\) is also a Pythagorean triplet.
Register for free to see more content