PDF chapter test TRY NOW
A scale factor is the ratio of similar figures' corresponding sides.
In the above theoretical material, we deal with similar triangles theoretically. Let us discuss how to construct a similar triangle using the concept of the scale factor. There are \(2\) cases.
Let us understand the cases using examples.
Example:
Case 1: If the scale factor is less than \(1\).
Construct a triangle similar to the given triangle \(PQR\) with its sides equal to \(\frac{2}{5}\) of the corresponding sides of the triangle \(PQR\).
Solution:
Given a triangle \(PQR\). We are required to construct another triangle whose sides are \(\frac{2}{5}\) of the corresponding sides of the triangle \(PQR\).
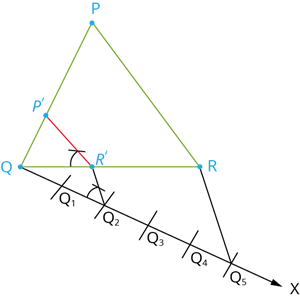
Construction:
Step 1: Construct a triangle \(PQR\) with any measurement.
Step 2: Draw a ray \(QX\) making an acute angle with \(QR\) on the side opposite to vertex \(P\).
Step 3: Locate \(5\) (the greater of \(2\) and \(5\) in \(\frac{2}{5}\)) points. \(Q_1\), \(Q_2\), \(Q_3\), \(Q_4\) and \(Q_5\) on \(QX\) so that \(QQ_1 = Q_1Q_2 = Q_2Q_3 = Q_3Q_4 = Q_4Q_5\).
Step 4: Join \(Q_5R\) and draw a line through \(Q_2\) (the second point, \(2\) being smaller of \(2\) and \(5\) in \(\frac{2}{5}\)) parallel to \(Q_5R\) to intersect \(QR\) at \(R'\).
Step 5: Draw a line through \(R'\) parallel to the line \(RP\) to intersect \(QP\) at \(P'\). Then, \(P'QR'\) is the required triangle, each of whose side is two - fifths of the corresponding sides of \(\triangle PQR\).
Let us consider the construction of triangle \(ABC\) using the scale factor \(\frac{3}{4}\).
Case 2: If the scale factor is greater than \(1\).
Construct a triangle similar to a given triangle \(PQR\) with its sides equal to \(\frac{3}{2}\) of the corresponding sides of the triangle \(PQR\).
Solution:
Given a triangle \(PQR\). We are required to construct an another triangle whose sides are \(\frac{3}{2}\) of the corresponding sides of the triangle \(PQR\).
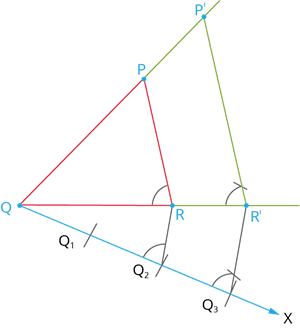
Construction:
Step 1: Construct a triangle \(PQR\) with any measurement.
Step 2: Draw a ray \(QX\) making an acute angle with \(QR\) on the side opposite to vertex \(P\).
Step 3: Locate \(3\) (the greater of \(2\) and \(3\) in \(\frac{3}{2}\)) points. \(Q_1\), \(Q_2\), and \(Q_3\) on \(QX\) so that \(QQ_1 = Q_1Q_2 = Q_2Q_3\).
Step 4: Join \(Q_2\) (the 2nd point, 2 being smaller of \(2\) and \(3\) in \(\frac{3}{2}\)) to \(R\) and draw a line through \(Q_3\) parallel to \(Q_2R\), intersecting the extended line segment \(QR\) at \(R'\).
Step 5: Draw a line through \(R'\) parallel to the line \(RP\) intersecting the extended line segment \(QP\) at \(P'\). Then, \(P'QR'\) is the required triangle, each of whose side is three - twos of the corresponding sides of \(\triangle PQR\).
Let us consider the construction of triangle \(ABC\) using the scale factor \(\frac{5}{3}\).
