5. Results on similar triangles

Let us learn a few results on the similarity of triangles.

  

1.

 

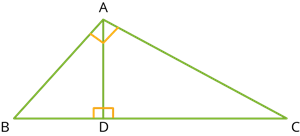
A perpendicular line drawn from the vertex of a right-angled triangle divides the triangle into two similar triangles and the original triangle.

 

Here, \(\triangle ADB \sim \triangle ADC\), \(\triangle BAC \sim \triangle BDA\), \(\triangle BAC \sim \triangle ADC\).

 

2.

 

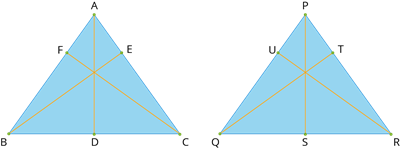
If two triangles are similar, then the corresponding sides' ratio is equal to the ratio of their corresponding altitudes.

 

That is, \(\triangle ABC \sim \triangle PQR\), then \(\frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} = \frac{AD}{PS} = \frac{BE}{QT} = \frac{CF}{RU}\)

 

3.

 

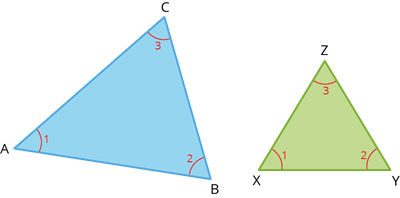
If two triangles are similar, then the corresponding sides' ratio is equal to the ratio of the corresponding perimeters' ratio.

 

That is, \(\triangle ABC \sim \triangle XYZ\), then \(\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX} = \frac{AB + BC + CA}{XY + YZ + ZX}\)

 

4.

 

The ratio of the area of two similar triangles equals the ratio of the squares of their corresponding sides.

 

That is, \(\frac{ar(\triangle ABC)}{ar(\triangle XYZ)} = \frac{AB^2}{XY^2} = \frac{BC^2}{YZ^2} = \frac{CA^2}{ZX^2}\)

 

5.

 

If two triangles have a common vertex and their bases are on the same straight line, the ratio between their areas is equal to the ratio between the length of their bases.

 

That is, \(\frac{ar(\triangle ABD)}{ar(\triangle ADC)} = \frac{BD}{DC}\)