4. Criteria of similarity

The following criteria are sufficient to prove that the two triangles are similar.

 

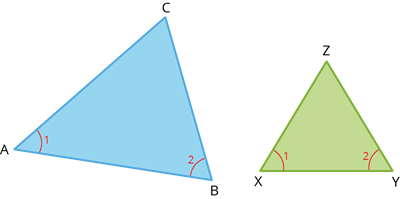
If two angles in a triangle and the two angles in the other triangle are equal, then the third angle in both triangles must be equal. Therefore, AA Similarity Criterion is the same as the AAA Similarity Criterion.

 

That is, \(\angle A = \angle X = \angle 1\), \(\angle B = \angle Y = \angle 2\) then \(\triangle ABC \sim \triangle XYZ\)

 

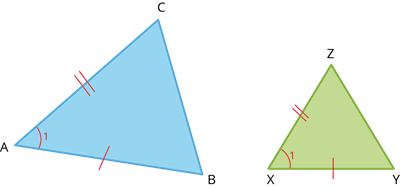
If one angle of a triangle is equal to one angle of another, and if the corresponding sides, including these angles, are proportional, then the two triangles are similar.

 

That is, \(\angle A = \angle X = \angle 1\) and \(\frac{AB}{XY} = \frac{AC}{XZ}\), then \(\triangle ABC \sim \triangle XYZ\)

 

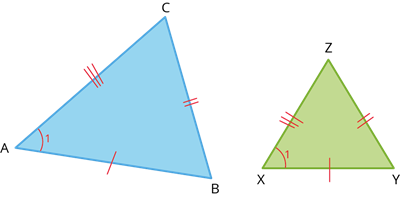
If the three sides of a triangle are proportional to the three corresponding sides of another triangle, then the two triangles are similar.

 

That is, \(\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX}\), then \(\triangle ABC \sim \triangle XYZ\)