PDF chapter test TRY NOW
Two figures are said to be congruent if they have the same shape and same size. Two figures are similar if they have the same shape but are not necessarily the same size.
Example:
A few examples of similar figures are:
1. 
2. 
3. 
Congruency and similarity of triangles
In congruency and similarity of triangles, \(3\) angles of one triangle are equal to \(3\) angles of the other triangle. The corresponding sides are equal in congruent triangles, whereas in similar triangles, the corresponding sides are proportional.
Let us differentiate the difference between congruence and similar triangles.
Congruent triangles | Similar triangles |
 |  |
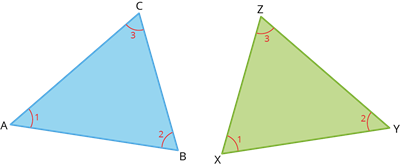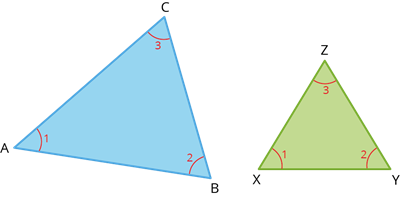\(\triangle ABC \cong \triangle XYZ\) | \(\triangle ABC \sim \triangle XYZ\) |
\(\angle A = \angle X\), \(\angle B = \angle Y\), \(\angle C = \angle Z\) | \(\angle A = \angle X\), \(\angle B = \angle Y\), \(\angle C = \angle Z\) |
\(AB = XY\), \(BC = YZ\), \(CA = ZX\) | \(AB =\neq XY\), \(BC \neq YZ\), \(CA \neq ZX\) |
\(\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX} = 1\) | \(\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX} < 1\) or \(> 1\) |
Same shape and same size. | Same shape but not same size. |
Important!
Two triangles are similar; if
(i) their corresponding angles are equal, and
(ii) their corresponding sides are in the same ratio (or proportion).
Consider two triangles \(ABC\) and \(PQR\) are similar. Then,
(i) \(\angle A = \angle P\), \(\angle B = \angle Q\) and \(\angle C = \angle R\) and
(ii) \(\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}\)
Register for free to see more content