4. Types of construction of triangle

Let us learn how to construct a triangle if the following are given.

 

1. The base, vertical angle and median on the base.

 

2. The base, vertical angle and altitude on the base.

 

3. The base, vertical angle and the point where the bisector of the vertical angle meets the base.

 

Let us consider the following construction.

 

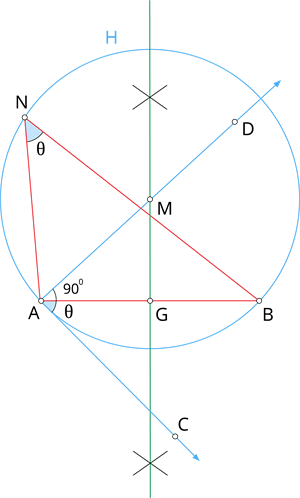
Construction:

 

Step 1: Draw a line segment \(\overline{AB}\).

 

Step 2: At \(A\), make \(\angle BAC = \theta\). Draw \(AC\).

 

Step 3: Draw \(AD \perp AC\).

 

Step 4: Draw the perpendicular bisector of \(AB\) meeting \(AD\) at \(M\).

 

Step 5: With \(M\) as centre and \(MA\) as radius, draw a circle \(ABH\).

 

Step 6: Take any point \(N\) on the circle; by the alternate segments theorem, the major arc \(ANB\) is the required segment of the circle containing the angle \(\theta\).