5. Construction of a triangle when its base, vertical angle and median are given

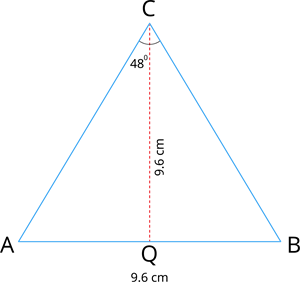
Construct a triangle \(ABC\) in which \(AB = 9.6 \ cm\), \(\angle C = 48^{\circ}\) and the median \(CQ\) from \(C\) to \(AB\) is \(9.6 \ cm\). Find the length of the altitude from \(C\) to \(AB\).

 

Solution:

 

First, let us draw a rough figure.

 

 

Construction:

 

 

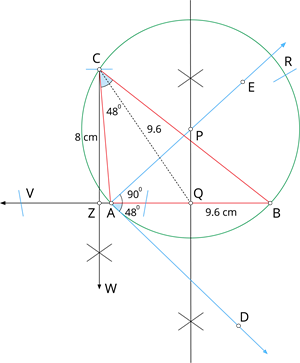
Step 1: Draw a line segment \(AB\) of length \(9.6 \ cm\).

 

Step 2: At \(A\), draw \(AD\) such that \(\angle DAB = 48^{\circ}\).

 

Step 3: At \(A\), draw \(AE\) such that \(\angle DAE = 90^{\circ}\).

 

Step 4: Draw the perpendicular bisector of \(AB\), which intersects \(AE\) at \(P\) and \(AB\) at \(Q\).

 

Step 5: Draw a circle with \(P\) as centre and \(AP\) as radius.

 

Step 6: From \(Q\), mark arcs of radius \(9.6 \ cm\) on the circle. Mark them as \(C\) and \(R\).

 

Step 7: Join \(AC\) and \(BC\). Thus, \(\triangle ABC\) is the required triangle.

 

Step 8: From \(C\), draw a line \(CW\) perpendicular to \(BV\). \(BV\) meets \(CW\) at \(Z\).

 

Step 9: The length of the altitude is \(CZ = 8 \ cm\).