PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us learn how to construct a triangle with an example when its base, vertical angle and altitude from the vertex to the base are given.
Example:
Construct a \(\triangle ABC\) such that \(AB = 5 \ cm\), \(\angle C = 45^{\circ}\), and the altitude from \(C\) to \(AB\) is of length \(2 \ cm\).
Solution:
First, let us draw a rough figure.
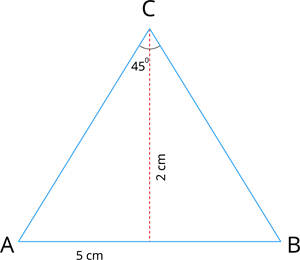
Construction:
Step 1: Draw a line segment \(AB\) of length \(5 \ cm\).
Step 2: At \(A\), draw \(AE\) such that \(\angle BAE = 45^{\circ}\).
Step 3: At \(A\), draw \(AD\) such that \(\angle EAD = 90^{\circ}\).
Step 4: Draw the perpendicular bisector \(XY\) to \(AB\), which intersects \(AD\) at \(G\) and \(AB\) at \(F\).
Step 5: With \(G\) as centre and \(GA\) as radius, draw a circle \(ABH\).
Step 6: From \(F\), mark an arc in the line \(XY\) at \(I\), such that \(FI = 2 \ cm\).
Step 7: Draw \(NM\) through \(I\), which is parallel to \(AB\).
Step 8: \(NM\) meets the circle at \(A\) and \(J\).
Step 9: Join \(AB\) and \(AC\). Thus, \(ABC\) is the required triangle.
Register for free to see more content