UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us look at our surroundings for a moment. We see glass tumblers, buckets, traffic cones in our day to day life. Do you know what shape is these all? If your answer is a cone, then it is wrong.
 |  |  |
The shape resembling in the above pictures is called the frustum of a cone.
If a smaller end of the cone is sliced by a plane parallel to its base, the portion of a solid between this plane and the base is known as the frustum of a cone.
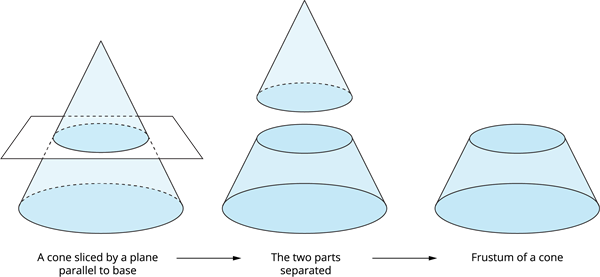
Surface area of a frustum of a cone
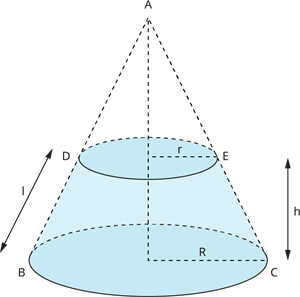
Let \(R\) and \(r\) be the radii of the bases \((R > r)\), \(h\) be the height, and \(l\) be the slant height of the frustum of a cone.
Curved surface area:
C. S. A. \(=\) \(\frac{1}{2}\) (sum of the circumferences of base and top region) \(\times\) slant height
\(=\) \(\frac{1}{2}(2 \pi R + 2 \pi r) l\)
\(=\) \(\frac{1}{2} \times 2 \pi (R + r) l\)
\(=\) \(\pi (R + r) l\)
Curved surface area of a frustum of a cone \(=\) \(\pi (R + r) l\), where \(l = \sqrt{h^2 + (R - r)^2}\) sq. units
Total surface area:
T. S. A. \(=\) Curved surface area \(+\) Area of the bottom circular region \(+\) Area of the top circular region
\(=\) \(\pi (R + r) l\) \(+\) \(\pi R^2 + \pi r^2\)
Total surface area of a frustum of a cone \(=\) \(\pi l(R + r)\) \(+\) \(\pi R^2 + \pi r^2\), where \(l = \sqrt{h^2 + (R - r)^2}\) sq. units
Reference:
Image by Clker-Free-Vector-Images from Pixabay
Register for free to see more content