UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreHemisphere
A section of the sphere cut by a plane through any of its great circles is a hemisphere. In another way, we can say, one half of a sphere is called a hemisphere.
Curved surface area:
C. S. A. \(=\) \(\frac{\text{Surface area of a sphere}}{2}\)
\(=\)
\(=\) \(2\pi r^2\)
Curved surface area of a hemisphere \(=\) \(2\pi r^2\) sq. units.
Total surface area:
T. S. A. \(=\) Curved surface area of a hemisphere \(+\) Area of the top region
\(=\) \(2\pi r^2\) \(+\) \(\pi r^2\)
\(=\) \(3 \pi r^2\)
Total surface area of a hemisphere \(=\) \(3 \pi r^2\) sq. units.
Hollow hemisphere
A hemisphere emptied from the inner side and has a difference in the outer and inner radius of a hemisphere is called a hollow hemisphere.
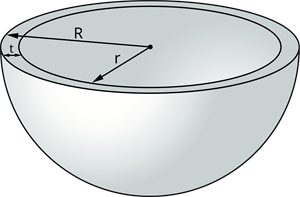
Curved surface area:
Let \(r\) be the inner radius and \(R\) be the outer radius of the hollow hemisphere.
The thickness of the hemisphere, \(t\) \(=\) \(R - r\)
C. S. A. \(=\) Area of an internal hemisphere \(+\) Area of an external hemisphere
\(=\) \(2 \pi R^2 + 2 \pi r^2\)
\(=\) \(2 \pi (R^2 + r^2)\)
Curved surface area of a hollow hemisphere \(=\) \(2 \pi (R^2 + r^2)\) sq. units
T. S. A. \(=\) Curved surface area of a hollow hemisphere \(+\) Area of the ring formed
\(=\) \(2 \pi (R^2 + r^2)\) \(+\) \(\pi R^2\) \(-\) \(\pi r^2\)
\(=\) \(2 \pi R^2 + 2 \pi r^2\) \(+\) \(\pi R^2\) \(-\) \(\pi r^2\)
\(=\) \(2 \pi R^2\) \(+\) \(\pi R^2\) \(+\) \(2 \pi r^2\)\(-\) \(\pi r^2\)
\(=\) \(3 \pi R^2\) \(+\) \(\pi r^2\)
\(=\) \(\pi(3R^2 + r^2)\)
Total surface area of a hollow hemisphere \(=\) \(\pi(3R^2 + r^2)\) sq. units
Important!
The properties of a hemisphere are same as the properties of a sphere.
Register for free to see more content