PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoSphere:
A sphere is a three-dimensional figure obtained by the revolution of a semicircle about its diameter as an axis.
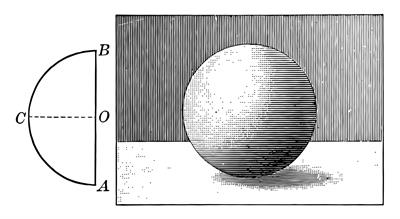
From the figure, \(ACB\) is a semicircle. If we rotate the semicircle \(ACB\) with diameter \(AB\) as an axis, we get the three-dimensional object sphere.
Properties of a sphere:
1. Sphere is made of all the points in the space which are equidistant from the fixed point called the centre.
2. Distance between the centre to the edge of the sphere is called the radius \((r)\) of the sphere.
3. Distance between any two points on a sphere through the centre is called the diameter \((d)\) of the sphere.
4. Diameter \(=\) \(2 \ \times\) radius
Surface area of a sphere:
Surface area of a sphere \(=\) \(4 \ \times\) Area of a circle
\(=\) \(4 \times \pi r^2\)
Surface area of a sphere \(=\) \(4 \pi r^2\) sq. units.
Important!
Every plane section of a sphere is a circle.
Surface area of a sphere - Archimedes Proof
The Greek mathematician Archimedes found that the surface area of a sphere is equal to the curved surface area of a cylinder having the same radius as the sphere and the height the length of the diameter of the sphere.
Let \(r\) be the radius of the sphere as well as cylinder.
Height of the cylinder \(=\) Diameter of the sphere \(=\) \(2r\)
Surface area of a sphere \(=\) Curved surface area of a cylinder
\(=\) \(2 \pi r h\)
\(=\) \(2 \pi r (2r)\)
\(=\) \(4 \pi r^2\)
Surface area of a sphere \(=\) \(4 \pi r^2\) sq. units.
Register for free to see more content