PDF chapter test TRY NOW
Let us learn the cartesian product of two sets in this article.
Illustration:
Let us consider the sets \(A\) and \(B\).
Where, \(A\) is the set of boys named \(1\), \(2\) and \(3\).
That is, \(A\) \(=\) \(\{1, 2, 3\}\).
And \(B\) is the set of girls named \(a\), \(b\) and \(c\).
That is, \(B\) \(=\) \(\{a, b, c\}\).
Let us see the possible ways of pairing each boy with a girl for the dance programme using an arrow diagram.
 |
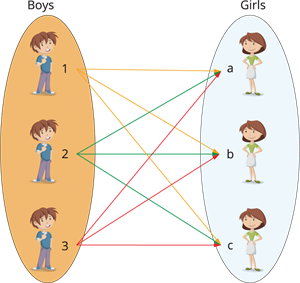We can select \(9\) distinct pairs as given below:
| \((1,a), (1,b), (1,c), (2,a), (2,b), (2,c), (3,a), (3,b), (3,c)\) |
Here, these pairs represent the cartesian product of the set of boys and the set of girls.
Based on the above illustration, we will define the Cartesian product of the sets \(A\) and \(B\) as follows:
Definition:
If \(A\) and \(B\) are two non-empty sets, then the set of all ordered pairs \((a, b)\) such that \(a \in A\), \(b \in B\) is called the Cartesian Product of \(A\) and \(B\), and is denoted by \(A \times B\).
Thus, \(A \times B\) \(=\) \(\{(a, b) | a \in A, b \in B\}\).
Important!
- \(A \times B\) is the set of all ordered pairs between the elements of the sets \(A\) and \(B\) where the first ordinate belongs to set \(A\) and the second ordinate belongs to set \(B\).
- \(B \times A\) is the set of all ordered pairs between the elements of the sets \(A\) and \(B\) where the first ordinate belongs to set \(B\) and the second ordinate belongs to set \(A\).
- If \(a = b\), then \((a, b) = (b, a)\).
- For any three sets \(A\), \(B\) and \(C\), the following properties are true.
- \(A \times (B \cup C)\) \(=\) \((A \times B) \cup (A \times C)\) (Distributive property over union).
- \(A \times (B \cap C)\) \(=\) \((A \times B) \cap (A \times C)\) (Distributive property over intersection).
Register for free to see more content