PDF chapter test TRY NOW
Illustration 1:
Consider the sets \(A\) and \(B\).
Let \(A\) \(=\) \(\{2, 3\}\) and \(B\) \(=\) \(\{1, 2, 3\}\).
We shall write the product \(A \times B\) as follows:
\(A \times B\) \(=\) \(\{(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)\}\)
The graphical illustration of \(A \times B\) is given by:
 |
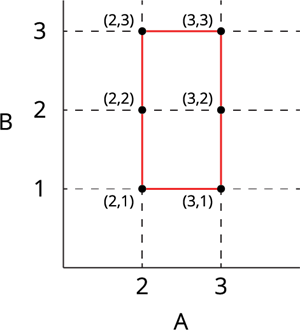Similarly, we will write the product \(B \times A\) as follows:
\(B \times A\) \(=\) \(\{(1, 2), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3)\}\)
The graphical illustration of \(B \times A\) is given by:
 |
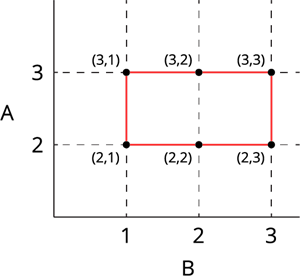From the graphs of \(A \times B\) and \(B \times A\), it is observed that \(A \times B\) \(\neq\) \(B \times A\).
- In general, \(A \times B\) \(\neq\) \(B \times A\) but \(n(A \times B)\) \(=\) \(n(B \times A)\).
- \(A \times B = \phi\) if and only if \(A = \phi\) or \(B = \phi\).
- If \(n(A) = x\) and \(n(B) = y\), then \(n(A \times B) = xy\).
Important!
Illustration 2:
Consider the sets \(A\) and \(B\).
Let \(A\) \(=\) \(\{\text{Set of all numbers in the interval } [2, 5]\}\) and \(B\) \(=\) \(\{\text{Set of all numbers in the interval } [4, 5]\}\).
The product \(A \times B\) corresponds to the intersecting region of the given intervals. In other words, it is the set of all points \((x,y)\) lying within the common region.
We shall represent the product \(A \times B\) graphically as follows:
 |
The product \(A \times B\) corresponds to the middle rectangular region. That is, it consists of all points \((x, y)\) within this rectangular region.
Important!
The product \(\mathbb{R} \times \mathbb{R}\) is called the cartesian plane, where it represents the set of all points \((x, y)\) where \(x\), \(y\) are real numbers.
Register for free to see more content