3. Composition of three functions

Let us learn the composition of three functions based on the composition of two functions.

 

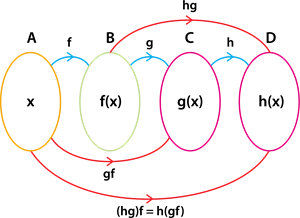
Consider the four sets \(A\), \(B\), \(C\) and \(D\).

 

Let \(f: A \rightarrow B\), \(g: B \rightarrow C\), \(h: C \rightarrow D\) be three functions.

 

The functions \(f\), \(g\) and \(h\) are composed as \(f \circ \left(g \circ h\right)\) and \(\left(f \circ g\right) \circ h\).

 

Here, we observe that three functions are involved in the composition. So, it is obvious that the composition of the functions is not commutative.

 

But the composition of three functions is always associative. That is equivalent to \(f \circ \left(g \circ h\right)\) \(=\)\(\left(f \circ g\right) \circ h\).

 

The composition of three functions is represented using an arrow diagram as follows: