UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreFibonacci number
\(1 + 1 = 2\)
\(1 + 2 = 3\)
\(2 + 3 = 5\)
\(5 + 8 = 13\)
\(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), …
Each number in a Fibonacci sequence is called a Fibonacci number.
Construction of Fibonacci sequence:
Step 1: The first two numbers are \(1\).
Step 2: The next numbers are found by adding up the two numbers before it.
Fibonacci spiral:
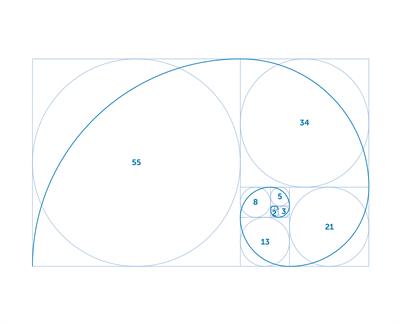
Fibonacci numbers in nature:
Lucas numbers
Lucas numbers are closely related to Fibonacci numbers. Fibonacci numbers starts with two \(1\)'s, but Lucas numbers start with \(1\) and \(3\), and the next numbers are obtained by adding the numbers before it.
Lucas sequence:
\(1 + 3 = 4\)
\(3 + 4 = 7\)
\(4+ 7 = 11\)
\(7 + 11 = 18\)
\(1\), \(3\), \(4\), \(7\), \(11\), \(18\), …
Each number in a Lucas sequence is called a Lucas number.
Golden Ratio
The golden ratio is denoted by the Greek letter \(\phi\), and the value is \(1.618\).
\(\phi = 1.681\)
It is surprising that if the sum of the two consecutive numbers in the Fibonacci sequence is divided by the larger number from the two successive number, you will get the number which is nearly equal to the golden ratio.
This spiral stairs follows a Fibonacci spiral pattern. This pattern is one of the reasons behind the elegant look of the stairs.
Register for free to see more content