5. Impact on adding a portion to a given shape

Consider a square whose side length is \(6\) \(cm\). Let us find the area and perimeter of the square.

Now, let us consider a right-angled triangle of base \(6\) \(cm\) and height \(8\) \(cm\) is attached to a rectangle. Find the perimeter and area of the given shape.

 

 

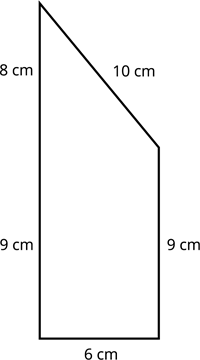
Solution:

 

Given:

 

The length of the rectangle \(=9\) \(cm\).

 

The breadth of the rectangle \(=6\) \(cm\).

 

The base of the triangle \(=6\) \(cm\).

 

The height of the triangle \(=8\) \(cm\).

 

To find the perimeter and the area of the square after adding a portion to the rectangle.

 

Perimeter of the given shape \(=\) Sum of all measures of outer length

 

Perimeter \(=(6+9+9+8+10)\) \(cm\)

 

Perimeter \(=42\) \(cm\)

 

Therefore, the perimeter of the given shape is \(42\) \(cm\).

 

Area of the given shape \(=\) Area of the rectangle \(+\) Area of the right triangle

 

Area \(=(l \times b)\) \(+ \frac{1}{2}(b \times h)\)

 

Area \(=(9 \times 6) +(\frac{1}{2}(6 \times 8))\)

 

Area \(=(54)+\) \((\frac{1}{2}\times 48)\)

 

Area \(=54+24\) \(=78\) \(sq. cm\)

 

Therefore, the area of the given shape is \(78\) \(sq. \ cm\).