4. Impact on removing a portion from a given shape

Let us consider an example to understand the concept.

 

Consider a square whose side length is \(6\) \(cm\). Let us find the area and perimeter of the square.

 

Area, \(A=s \times s\)

 

\(A=6 \times 6\)

 

\(A=36\) \(sq. cm\)

 

Perimeter, \(P=4s\)

 

\(P=4\times 6\)

 

\(P=24\) \(cm\)

 

Now, let us cut a rectangle of length \(3 \ cm\) and breadth \(2 \ cm\) from the corner of the square and find the perimeter and area of the given shape.

 

 

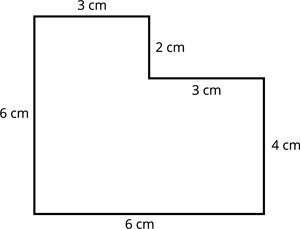
Solution:

 

Given:

 

The side length of the square \(=6 \ cm\).

 

The length of the rectangle \(=3 \ cm\).

 

The breadth of the rectangle \(=2 cm\).

 

To find the perimeter and area of the square after removing the rectangle.

 

Perimeter of the given shape \(=\) Sum of all measures of outer length

 

Perimeter \(=\) \((3+6+6+4+3+2)\) \(cm\)

 

Perimeter \(=24\) \(cm\)

 

Therefore, the perimeter of the given shape is \(24\) \(cm\).

 

Area of the given shape \(=\) Area of square \(-\) Area of rectangle

 

Area of the given shape \(=\) \(s \times s\) \(-\) \(l \times b\)

 

\(=\) \(6 \times 6\) \(-\) \(3 \times 2\) \(sq. \ cm\)

 

\(= 36-6\) \(sq. cm\)

 

\(=30\) \(sq. cm\)

 

Therefore, the area of the given shape is \(30\) \(sq. \ cm\).

 

Here, the perimeter is not changed, but the area is decreased.