UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreWhat is the area of the combined shape?
The area of combined shape is same just like finding the area of all the other shapes. The area of combined shape is the sum of all the area of the shapes from which the combined shape is made.
Example:
Let us consider an example to understand the concept clearly.
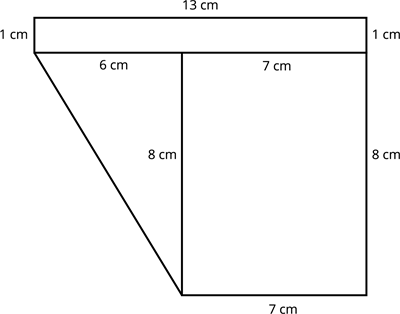
Area of the combined shape \(=\) Area of the rectangle \(1\) \(+\) Area of the triangle \(+\) Area of the rectangle \(2\)
Area of the rectangle \(1\) \(=l \times b\)
\(=13 \times 1\) \(=13\) \(sq. cm\)
Area of the rectangle \(2\) \(=l \times b\)
\(=8 \times 7\) \(=56\) \(sq. cm\)
Area of the triangle \(=\frac{1}{2}(b \times h)\)
\(=\frac{1}{2}(6 \times 8)\) \(=\frac{1}{2}(48)\) \(=24\) \(sq. cm\).
Now, adding all these area, we have:
Area of the combined shape \(=13+24+56\) \(sq. cm\) \(=93\) \(sq. cm\).
Therefore, the area of the combined shape is \(93\) \(sq. cm\).
Register for free to see more content