UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn our previous classes, we have already studied that multiplication operation can be performed in different ways. We know that multiplication is a continues addition process, and it is commutative.
Now we take grid model to multiply the monomials and understand the geometrical approach to the monomial's multiplication.
Example:
Consider the below square \(4 × 5\), which has \(4\) rows and \(5\) columns. And it comprises \(20\) small squares.
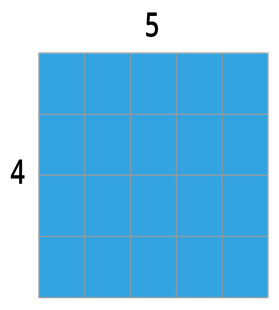
Similarly, observing the below square \(5 × 4\) , it has \(5\) rows and \(4\) columns, this is also consists \(20\) small squares.
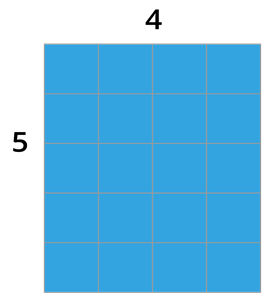
Therefore, multiplication is commutative \(4 × 5 = 5 × 4 = 20\).
Here, we used a grid model to represent multiplication. We can represent the same using the area model.
Area model:
The area model simplifies multiplication by dividing large rectangle areas into smaller rectangle areas. Also, the same example which is discussed above may be decomposed as:
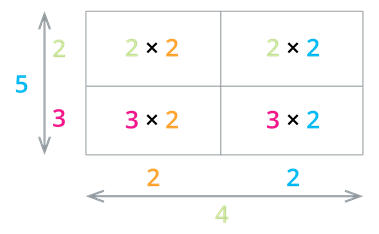
The decomposition method, which we discussed above, is very useful when we are finding the product of large numbers.
Now, we extend this concept to the multiplication of variables.
Let us consider the below biscuit as a rectangular-shaped object, each part of a rectangular-shaped of length ‘\(x\)’ units and breadth ‘\(y\)’ units. Also, the area of one part of the biscuit is '\(xy\)' square units.

The \(6\) parts of the biscuit create a rectangular shape. The area of each part is \(xy\), hence the area of the shape is \(6 × xy = 6xy\)………………..\((1)\)
We can obtain the same area by taking the length of the rectangular shape as \(x +x +x = 3x\) and breadth as \(y + y = 2y\).

Hence, its area \(= 3x × 2y\)………………..\((2)\)
Here, we can see that both the equation are equal. \(6xy = 3x × 2y\). So, we can conclude that both the geometrical representation of variables gives the same result.
In the next lesson, we get to know about the geometrical proof of identities.
Reference:
https://www.shutterstock.com/image-photo/piece-biscuit-81641635