PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoWhen it comes to solving the algebraic equation, identities play a vital role to solve them. In this lesson, we are going to explore the geometrical proof of identities.
Let us first see the varies identities which we will discuss here:
1.
2. \((a + b^2) = a^2 + 2ab + b^2\)
3. \((a - b^2) = a^2 - 2ab + b^2\)
4.
Let us take each identity one by one and discuss the proof of that identity.
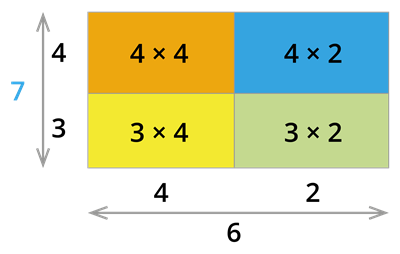
By observing the above rectangle, we can notice that:
\(\text{Area of the bigger rectangle}\) \(=\) \(\text{Area of a square (Orange)}\) \(+\) \(\text{Area of three rectangles}\)
\((4 + 3)\) \((4 + 2)\) \(=\) \((4 × 4) + (4 × 2) + (3 × 4) + (3 × 2)\)
Now, we simplify the LHS and RHS of the above expression.
LHS \(=\) \((4 + 3)\) \((4 + 2)\) \(=\) \(7×6 = 42\)
RHS \(=\) \((4 × 4) + (4 × 2) + (3 × 4) + (3 × 2)\)
RHS \(=\) \(16+8+12+6 = 42\)
Therefore, LHS \(=\) RHS
Similarly, if we use the variables in this case instead of number we get:
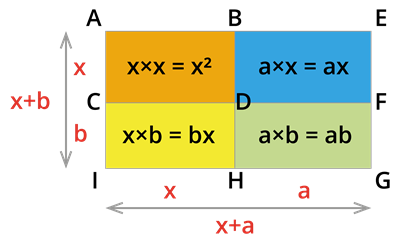
Let one side of a rectangle be \((x +a)\), and the other side be \((x + b)\) units.
Then, \(\text{the total area of the rectangle }AEGI\) \(=\) \(\text{length } \times \text{breadth}\) \(=\) \((x+a)(x+b)\)………….\((1)\)
\(\text{The area of the rectangle }AEGI\) \(=\) \(\text{The area of the square }ABCD\) \(+\) \(\text{The area of the rectangle }BEFD\) \(+\) \(\text{The area of the rectangle }DFGH\) \(+\) \(\text{The area of the rectangle }CDHI\).
\(\text{The area of the rectangle AEGI}\) \(=\)
……………..\((2)\)
From the equation, \((3)\) and \((4)\) we get .
Therefore, is a identity.
Example:
Simplify the expression using the identity .
The expression is .
The expression is .
Now write the given expression with respect to the given identity \((x+a)(x+b)\) \(=\) \(x^2+(a+b)x+ab\).
Now simplify the expression.
.
Therefore, \(=\) .
Register for free to see more content