
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us discuss an activity to learn the key terms related to mirrors.
- Hold a concave mirror in your hand and face the Sun with its reflecting surface.
- Using a sheet of paper, hold close to the mirror and direct the light reflected onto a sheet of paper.
- Gradually move the sheet of paper back and forth until you find a bright, sharp spot of light on it.
- For a few minutes, keep the mirror and the paper in the same position.
What are your observations?
At first, the paper begins to burn and produces smoke. It is possible that it will catch fire at some point.
What causes it to catch fire?
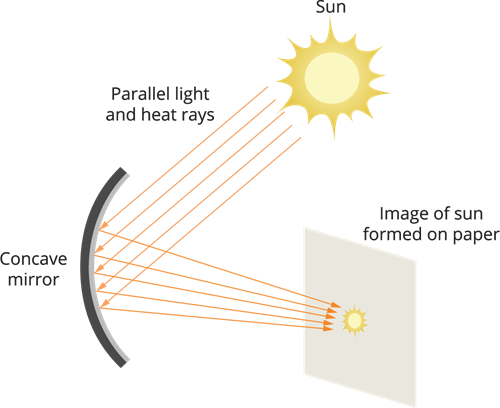
Converging the light rays using concave mirror
The Sun's light is converged at a point by the mirror, creating a sharp, bright spot. In fact, the image of the Sun on the sheet of paper is this bright spot. The concave mirror's focus is at this location. The paper is ignited by the heat produced by the concentrated sunlight. The distance between this image and the mirror's position gives an estimate of the mirror's focal length.
Let's use a ray diagram to try to understand this observation.
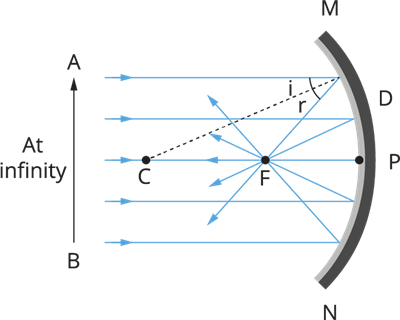
Object at infinity
A concave mirror receives a number of rays that are parallel to the principal axis. Examine the rays that have been reflected. They all meet/intersect at a point along the mirror's principal axis.
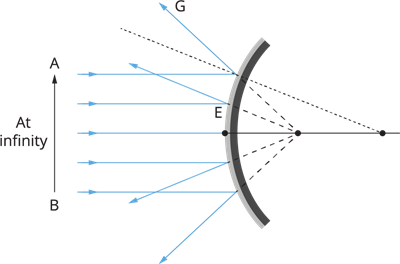
Object at infinity
In what way a convex mirror reflect rays parallel to the principal axis?
The rays that are reflected appear to be coming from a point on the principal axis. The principal focus of the convex mirror is this point. The letter \(F\) stands for the main point of focus. The focal length of a spherical mirror is the distance between the pole and the principal focus.
The aperture of a spherical mirror is the diameter of the reflecting surface. The aperture is represented by the distance \(MN\). Only spherical mirrors with an aperture smaller than their radius of curvature will be considered in this discussion.
Is there a relationship between a spherical mirror's radius of curvature \(R\) and focal length \(f\)?
The radius of curvature of small aperture spherical mirrors is found to be equal to twice the focal length.
\(R\) \(=\) \(2f\)
This indicates that the principal focus of a spherical mirror lies midway between the pole and centre of curvature.