PDF chapter test TRY NOW
In the previous section, we learned the different applications of torque.
In this section, we will discuss the principle of moments.
Principle of Moments:
Whenever a number of like or unlike parallel forces are acting on a rigid body, and the body is in a state of equilibrium, then the algebraic sum of the moments in the clockwise direction is equal to the algebraic sum of the moments in the anticlockwise direction.
In different words, When the body is in an equilibrium state, the algebraic sum of the moments of all the individual forces about any point is equal to zero.
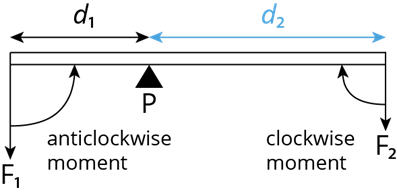
In the above figures, the force \(F_1\) creates an anticlockwise rotation at a distance \(d_1\) from the point of pivot (\(P\)) (known as 'fulcrum'), and the force \(F_2\) creates a clockwise rotation at a distance \(d_2\) from the pivot point (\(P\)).
The principle of moments can be expressed as follows:
Register for free to see more content