PDF chapter test TRY NOW
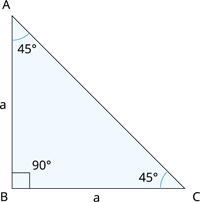
சமபக்க முக்கோணம் \(ABC\) யின் கோணம் \(45^{\circ}\) மேலும் \(B\) யில் செங்கோணம்.
முக்கோணத்தின் பக்க அளவு \(a\) அலகுகள்.
முதலில் கர்ணத்தின் அளவினை கணக்கிடுக.
பிதாகர்ஸ் தேற்றத்தின் படி:
செங்கோண முக்கோணத்தில் , \(\text{கர்ணம்}^{2} = \text{அடுத்துள்ள பக்கம்}^{2} + \text{எதிர்பக்கம்}^{2}\).
\(AC^2\) \(=\) \(AB^2\) \(+\) \(BC^2\).
\(AC^2\) \(=\) \(a^2\) \(+\) \(a^2\)
\(AC^2\) \(=\) \(2a^2\)
\(\Rightarrow AC\) \(=\) \(\sqrt{2a^2}\)
\(AC\) \(=\) \(a \sqrt{2}\) அலகுகள்
எனவே, செங்கோண மற்றும் சமபக்க முக்கோணத்தில் :
எதிர் பக்கம் \(=\) \(a\) அலகுகள்
அடுத்துள்ள பக்கம் \(=\) \(a\) அலகுகள்
கர்ணம் \(=\) \(a \sqrt{2}\) அலகுகள்
முக்கோணவியல் விகிதங்கள் - கோண அளவு \(45^{\circ}\).
- Sine \(45^{\circ}\):
\(\sin 45^{\circ}\) \(=\) \(\frac{\text{எதிர்பக்கம் }}{\text{கர்ணம்}}\)
\(=\) \(\frac{a}{a \sqrt{2}}\)
\(=\) \(\frac{1}{\sqrt{2}}\)
- Cosine \(45^{\circ}\):
\(\cos 45^{\circ}\) \(=\) \(\frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}}\)
\(=\) \(\frac{a}{a \sqrt{2}}\)
\(=\) \(\frac{1}{\sqrt{2}}\)
- Tangent \(45^{\circ}\):
\(\tan 45^{\circ}\) \(=\) \(\frac{\text{எதிர் பக்கம்}}{\text{அடுத்துள்ள பக்கம்}}\)
\(=\) \(\frac{a}{a}\)
\(=\) \(1\)
இவற்றை பயன்படுத்தி முக்கோணவியலின் விகிதங்களின் தலைகீழிகளை காணலாம்:
- Cosecant \(45^{\circ}\):
\(\text{cosec}\,\theta\) \(=\) \(\frac{1}{\sin \theta}\)
\(=\) \(\sqrt{2}\)
- Secant \(45^{\circ}\):
\(\sec \theta\) \(=\) \(\frac{1}{\cos \theta}\)
\(=\) \(\sqrt{2}\)
- Cotangent \(45^{\circ}\):
\(\cot \theta\) \(=\) \(\frac{1}{\tan \theta}\)
\(=\) \(1\)
முக்கோணவியல் விகிதங்கள் - கோண அளவு \(45^{\circ}\) க்கான அட்டவணை.
\(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) | \(\text{cosec}\,\theta\) | \(\sec \theta\) | \(\cot \theta\) | |
\(\theta = 45^{\circ}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{\sqrt{2}}\) | \(1\) | \(\sqrt{2}\) | \(\sqrt{2}\) | \(1\) |
Register for free to see more content